知识库 > Tinysoft代码优化 > 2 优化技巧
2.3 矩阵运算
- 矩阵操作符的运算速度远远快于for循环,例如求矩阵的乘法。A := Rand(300,300);
B := Rand(300,300);
Mult := array();
Mtic ;
For i := 0 to mrows(A)-1 do
For j :=0 to mcols(B)-1 do
Multi[i,j] := sum(a[i]*b[:,i]);
T1 := Mtoc;
Mtic ;
Mult := A :* B;
T2 := Mtoc;
Return array('循环所用时间':t1,"操作符所用时间":t2); //结果对比
结果: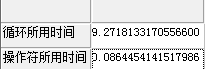
从结果中可以看出,矩阵操作符的运算速度是循环的100倍。优化了算法,复杂度小于n^3,远远小于循环, 当数据量扩大时这种优势就会更加明显。
因为TSL主要采取行储存的方式,所以对于二维数组的行操作快于列操作,例如求一个1000*1000的方阵各行的和与各列的和。X := Rand(1000,1000) ;
Sumr := array();
Mtic ;
For i := 0 to mrows(X)-1 do
Sumr[i] := sum(X[i]);
T1 := Mtoc;
Mtic ;
For i := 0 to mcols(X)-1 do
Sumr[i] := sum(X[:,i]);
T2 := mtoc;
Return array('行操作时间':t1,"列操作时间":t2); //结果对比
结果: