知识库 > 数学方法 > 统计分布
泊松分布
- 泊松分布适合于描述单位时间内随机事件发生的次数.如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数等等.
泊松分布的概率函数为:
泊松分布的参数 是单位时间(或单位面积)内随机事件的平均发生率.
是单位时间(或单位面积)内随机事件的平均发生率.
服从泊松分布的随机变量,其数学期望与方差相等,同为参数 :
: 
在二项分布的伯努力试验中,如果试验次数n很大,二项分布的概率p很小,且乘积 比较适中,则事件出现的次数的概率可以用泊松分布来逼近.事实上,二项分布可以看作泊松分布在离散时间上的对应物.
比较适中,则事件出现的次数的概率可以用泊松分布来逼近.事实上,二项分布可以看作泊松分布在离散时间上的对应物.
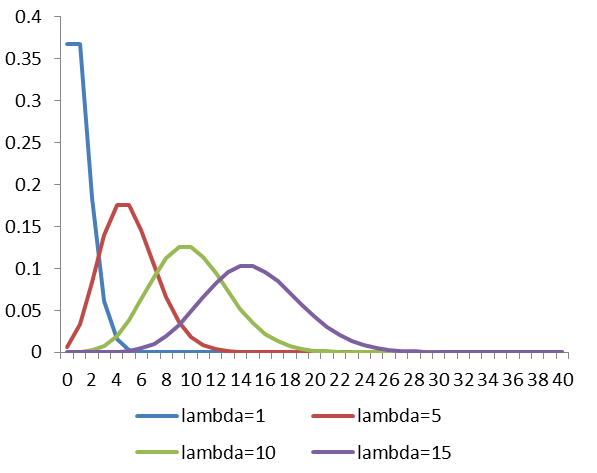
泊松分布概率函数
最大似然估计:给定n个样本值 ,希望得到从中推测出总体的泊松分布参数
,希望得到从中推测出总体的泊松分布参数 的估计.为计算最大似然估计值,列出对数似然函数:
的估计.为计算最大似然估计值,列出对数似然函数:

对函数 取相对于
取相对于 的导数并令其等于零:
的导数并令其等于零:

解得 从而得到一个驻点:
从而得到一个驻点:

sf_ poisspdf (x:array,lambda:real,v:array)
sf_poisscdf (x:array, lambda:real,v:array)
sf_poissinv (y:array,lambda:real, v:array)
Randpoiss (lambda:Real,row:Integer,col:Integer)
poissfit(x:array,alpha:Real);
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
lambda:分布参数,实数;
v:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
alpha:显著性水平,为0,1之间的实数,缺省为0.05