要使普通最小二乘法是估计多元线性回归模型的理想方法，我们需要有7-1中的5个基本假设。但是在实际应用中，大多数情况是不能满足这五个5个基本假设的，这个时候，普通最小二乘法就不能得到无偏有效的参数估计量了。
多重共线性，解释变量之间存在线性关系违背了解释变量间不相关的经典假设，将会给普通最小二乘法带来严重后果。
完全多重共线，即存在不全为0的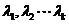使式7.16成立。

不完全多重共线，即存在不全为0的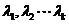使上式成立。
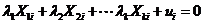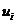(为随机干扰项)
一般的，统计数据中的多个解释变量之间基本都存在一定程度的相关性，但是完全多重共线性一般是用户人为错误造成。
当解释变量之间存在多重共线性，仍然使用最小二乘法估计参数会产生很多不良后果。
1：完全共线下参数估计不存在，这一种情况下，应该把变量合并，或去除。
2：近似共线性下虽然参数估计是无偏估计，但是参数估计量的方差变大

3：参数估计量经济含义不合理。实践表明，如果出现参数估计量的经济意义不合理，应该首先怀疑是否存在多重共线性。
4：变量的显著性检验和模型的预测功能失去意义。
检验多重共线性的方法主要有
1：解释变量间的相关系数
除相关矩阵对角线上的元素外，看是否有元素很大（一般与0.8比较），需要说明，相关系数大的一定存在多重共线，但是相关系数小的不一定没有多重共线。
2：判定系数法
设有解释变量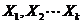的回归模型为：
 
为了诊断多重共线性，使模型中每一个解释变量分别以其余解释变量作为解释变量构造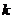个回归方程


…….

对这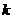个回归方程进行参数估计，并计算样本决定系数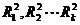。如果这些可决系数中的最大者接近于1，譬如说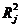，那么说明该解释变量可以用其他解释变量的线性组合代替，即存在多重共线性，旦有可能导致式（3-4）出现严重的多重共线性，之所以说有可能是因为可决系数也受样本容量影响。
3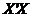：特征值判别
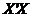有多少个特征根接近于零，矩阵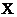就有多少个多重共线关系，并且这些多重共线关系的系数向量就等于接近于零的那些待征根对应的持征向量。
4：条件数判别
我们称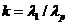为方针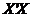的条件数，利用条件数可以度量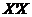特征值的散步程度，可以用来判断多重共线性的是否存在以及多重共线性的严重程度。一般我们认为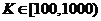有强多重共线性，有严重的多重共线性。
5：方差扩大因子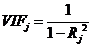
:
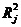：使用第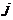个解释变量对其余变量做线性回归时的可决系数。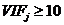则认为存在严重的多重共线性。
有时也是有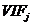的均值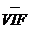来衡量，如果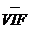远大于1，则认为存在严重多重共线性。