TSL语言基础 > 矩阵计算 > 矩阵运算
三目运算符.?:
- 支持矩阵,可以对fmarray或array的单元格进行判别,组装出对应的矩阵,这样的做法可以避免有些需要循环判别的矩阵操作。对于全数字而言,以前实现需要使用bool矩阵和值矩阵相乘后相加来完成:如(a.>3) * a1 + (a.<=3)*a2,或者采用mfind得到的数组取子矩阵来操作。
新的支持会使得这种操作极为便捷,也符合思维定式
例如a:=array(1,2,3,4,5);
b:=a.>3 .? array(2,3,4,5,6) : array(3,4,5,6,7)
b的结果为:array(3,4,5,5,6)
即,对集合a中每个元素的集进行判断取值,然后得到对应的结果返回到结果集中。
同样,这种方式也支持FMArray。
但是需要注意,当f.?A:B中,A与B都是FMArray时,两者的维度与大小必须是一致的。
当A与B的单元数据类型不一致时,也符合FMArray矩阵合并时对单元格数据类型的包容处理规则。
例如:将矩阵f1中不大于3的值用矩阵f2中的元素替换
f1:=fmarray[[1,2],[0,4],[1,2],[5,6]];
f2:=fmarray[[100,10],[200,20],[300,30],[400,40]];
b:=f1.>3 .? f1:f2;
return b;
结果: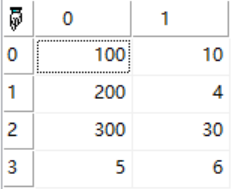
例如:将整型矩阵中不符合条件的值用浮点数10.5替换
f1:=fmarray[[1,2],[0,4],[1,2],[5,6]];
b:=f1.>3 .? f1:10.5;
return b;
返回的矩阵中,所有单元格类型都为浮点数: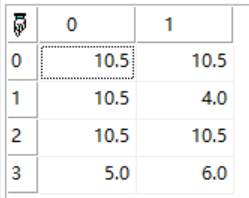
注:即便判断中没有出现符合条件的单元,数据类型不同时也会做包容处理。