TSL语言基础 > 数学与统计教程 > 多元统计分析
主成分分析
- 主成分分析:将原来较多的指标简化为少数几个新的综合指标的多元统计方法。这几个新的综合变量就是主成分,而关于主成分的实际意义,要结合具体问题和有关专业知识才能给出合理的解释。
主成分分析得到的主成分与原始变量之间的关系(正交变换):
>>主成分保留了原始变量绝大多数信息。
>>主成分的个数大大少于原始变量的数目。
>>各个主成分之间互不相关。
>>每个主成分都是原始变量的线性组合。
假设我们所讨论的实际问题中,有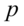 个指标,我们把这
个指标,我们把这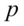 个指标看作
个指标看作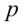 个随机变量,记为
个随机变量,记为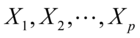 ,主成分分析就是要把这
,主成分分析就是要把这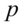 个指标的问题,转变为讨论这
个指标的问题,转变为讨论这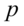 个指标的线性组合的问题,而这些新的指标
个指标的线性组合的问题,而这些新的指标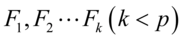 ,按照保留主要信息量的原则充分反映原指标的信息,并且相互独立。
,按照保留主要信息量的原则充分反映原指标的信息,并且相互独立。
在二维坐标下,主成分分析就是进行了一个坐标轴的平移和旋转(如图4-1,4-2),平移使原点,放在数据的中心点,旋转使数据在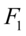 上的离散程度(方差)达到最大,
上的离散程度(方差)达到最大,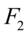 在与前面主成分保持正交的情况下离散程度最大。
在与前面主成分保持正交的情况下离散程度最大。
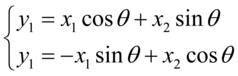 (4.1)
(4.1)
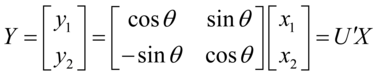 (4.2)
(4.2)
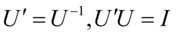 ,
, 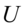 为正交矩阵
为正交矩阵
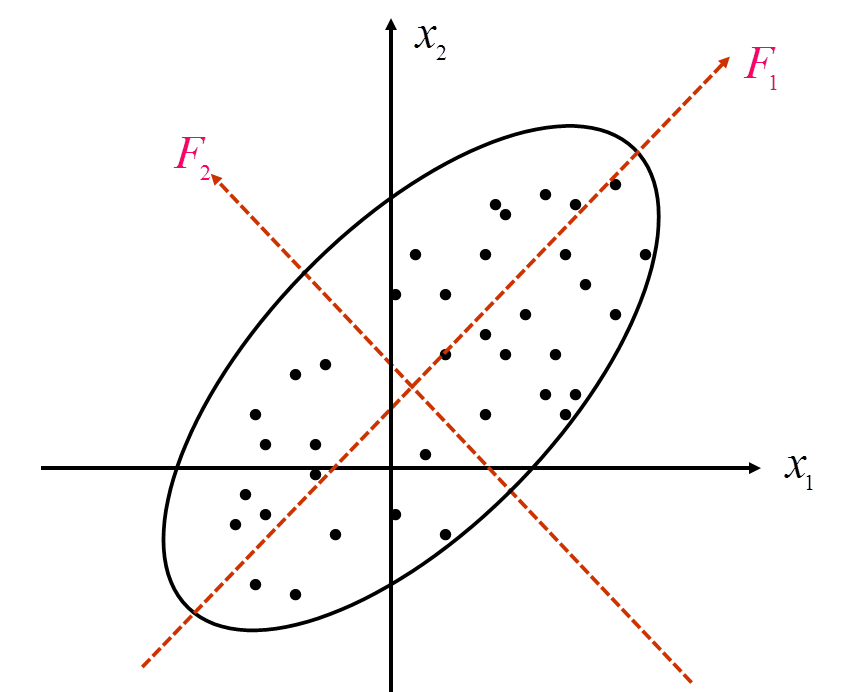
图4-1 二维坐标系下的主成分图4-2二维坐标系下的主成分
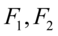 除了包含
除了包含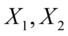 中的信息起着浓缩作用之外,还具有不相关的性质,这就使得在研究复杂的问题时避免了信息重叠所带来的虚假性(多重共线性)。二维平面上的个点的方差大部分都归结在
中的信息起着浓缩作用之外,还具有不相关的性质,这就使得在研究复杂的问题时避免了信息重叠所带来的虚假性(多重共线性)。二维平面上的个点的方差大部分都归结在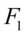 轴上,而
轴上,而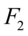 轴上的方差很小。
轴上的方差很小。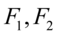 称为原始变量
称为原始变量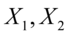 的综合变量.
的综合变量. 简化了系统结构,抓住了主要矛盾。
简化了系统结构,抓住了主要矛盾。
计算主成分有两种情况,当分析中所选择的经济变量具有不同的量纲,变量水平差异很大,应该选择基于相关系数矩阵的主成分分析,否则,我们基于协方差做就可以了。
1)基于协方差计算主成分
a)求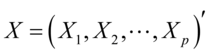 的协方差
的协方差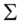
b)对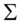 进行特征值分解,得到递减的特征值序列
进行特征值分解,得到递减的特征值序列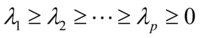 以及对应的特征向量
以及对应的特征向量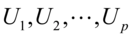 。并依据累计贡献率选出前
。并依据累计贡献率选出前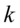 个特征值。
个特征值。
其中最大特征根的特征向量对应第一主成分的系数向量;第二大特征根对应的特征向量是第二大主成分的系数向量
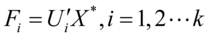
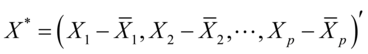
c)载荷矩阵: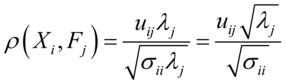
2)基于相关系数计算
a)对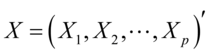 进行Z分数标准化得到
进行Z分数标准化得到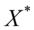 ,再求协方差
,再求协方差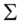
b)对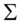 进行特征值分解,得到递减的特征值序列
进行特征值分解,得到递减的特征值序列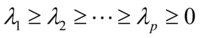 以及对应的特征向量
以及对应的特征向量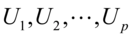 。并依据累计贡献率选出前
。并依据累计贡献率选出前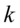 个特征值。
个特征值。
其中最大特征根的特征向量对应第一主成分的系数向量;第二大特征根对应的特征向量是第二大主成分的系数向量
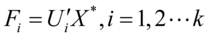
c)载荷矩阵: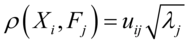
主成分分析模型:princomp