因子分析和主成分分析一样，也是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。
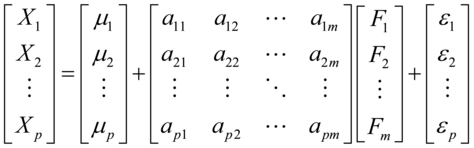        (4.3)
      
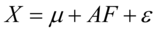
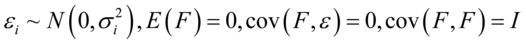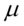  ，是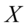的均值向量.
  该模型被称为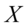有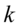个因子的因子分析模型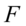，为公共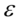因子，特殊因子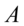，为因子载荷矩阵。
  由以上的关系我们知道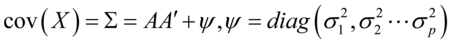，从而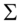对角线上的元素
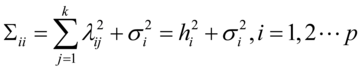             (4.4)
  其中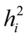反映了公共因子对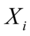的影响，称之为共同度.
  值得注意的是，因子分析并不是唯一的，若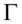是任意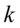阶正交阵，则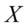可以表示成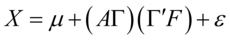：，将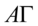作为因子载荷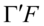，作为公共因子，则因子分析的条件依然满足，因子载荷的不唯一性，使得我们有更多的选择的余地，对于我们的分析反而是有利的。
  提取因子的方法有多种，常见的有主成分分析，主因子分析，迭代主因子分析，极大似然分析。旋转的方法更是种类繁多，主要有最大方差，最大均方。由于提取因子的随机性，通过旋转公因子可以减少这种随意性，所以公共因子旋转式必要的，旋转同时也有利于公共因子现实意义的解释。

因子分析模型：Factor