TSL语言基础 > 数学与统计教程 > 统计分布
统计分布简介
- 介绍统计各种分布函数前,我们先简单的介绍下概率论理论下常使用的几个函数:
1)perms
列出样本的所有排列或者排列的种类perms (array('a','b','c','d'));//返回'a','b','c','d'的各种排列方式 perms(5);//计算 5个样品的排列数目2)Nchoosek
Nchoosek 列出抽样的各种情况或者抽样的种类数目Nchoosek (array('a','b','c','d'),2); //返回'a','b','c','d'中抽取2个样本的所有组合3)gamma
Nchoosek (5,3);//计算 5个样品中抽出3个样品的组合数目
Gamma函数,使用gamma函数可以计算阶乘:Return gamma(5); //计算的是5-1的阶乘TinySoft金融分析平台上提供了有关统计分布的函数:概率密度,(累计)分布函数,分位数函数(分布逆函数),随机数函数,估计函数。主要函数都罗列在表5-1中.
表5-1 分布函数汇总概率密度 分布函数 分布逆函数 随机数 估计函数 离散均匀分布 sf_unidpdf sf_unidcdf sf_unidinv randunid 几何分布 sf_geopdf sf_geocdf sf_geoinv Randgeo 超几何分布 sf_hygepdf sf_hygecdf sf_hygeinv Randhyge 二项分布 sf_binopdf sf_binocdf sf_binoinv Randbino binofit 负二项分布 sf_nbinpdf sf_nbincdf sf_nbininv Randnbin 均匀分布 sf_unifpdf sf_unifcdf sf_unifinv Randunif uniffit 泊松分布 sf_poissonpdf sf_poissoncdf sf_poissoninv Randpoisson poissfit 指数分布 sf_exppdf sf_expcdf sf_expinv Randexp expfit 正态分布 sf_normpdf sf_normcdf sf_norminv Randnorm 卡方分布 sf_ch2pdf sf_ch2cdf sf_ch2inv Randch2 学生T分布 sf_tpdf sf_tcdf sf_tinv1 Randt F分布 sf_fpdf sf_fcdf sf_finv1 Randf gam分布 sf_gampdf sf_gamcdf sf_gaminv Randgam beta分布 sf_betapdf sf_betacdf sf_betainv1 Randbeta 瑞利分布 sf_raylpdf sf_raylcdf sf_raylinv1 Randrayl1 威布尔分布 sf_wblpdf sf_wblcdf sf_wblinv Randwbl 对数正态分布 sf_lognpdf sf_logncdf sf_logninv Randlohn 拉普拉斯分布 sf_Laplacepdf sf_Laplacecdf sf_Laplaceinv RandLaplace 柯西分布 sf_Cauchypdf sf_Cauchycdf sf_Cauchyinv RandCauchy
函数命名规则:
图5-1分布函数常用命名规则
我们的概率分布函数(包括概率密度函数,分布函数,分布逆函数)输入的第一个变量参数是随机变量或分布函数值,都支持数组形式,中间的参数,一般为分布参数,参数个数不定,只支持符合要求的实数和整数类型.最后一个参数存在的主要原因是为了支持tinysoft金融分析平台以前的使用方法,该参数可缺省,而使用return输出结果,输出结果和第一个参数的维度是一样的.
生成随机数的函数名称一般使用rand+分布类型(分布参数+行数目+列数目).
如:return randrayl(5,array('a','b','c')); return randrayl(5,array('a','b','c','d','e','f'),4);
return randrayl(5,4,array('a'));
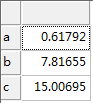
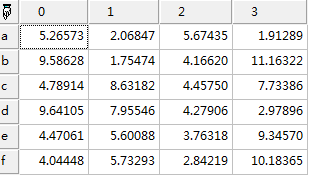
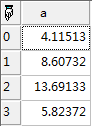
图5-2生成瑞利分布随机数
或使用rand函数:A:=rand(100,100,array("normal")); //标准正态分布 a := rand(100,100,array("normal",0,1));//标准正态分布支持如下类型(大小写无关):正态分布"normal",泊松分布"posisson",伽马分布"Gamma",均匀分布"Uniform",二项分布"Binomial",几何分布"Geometric",指数分布"Exp",beta分布"Beta",对数正态分布"Lognormal",威布尔分布"Weibull",柯西"Cauchy",拉普拉斯"Laplace",超几何"Hypergeometric",离散均匀"IntUniform",瑞利分布"Rayleigh"
估计函数的函数名称一般使用分布类型+fit(数据+显著性水平)如
return normfit(rand(1000,5),0.05);
结果以列为样本进行估计,muhat,muci为正态分布位置参数的点估计,区间估计,sigmahat,sigmaci为正态分布形态参数的点估计,区间估计.其中每一个样本区间的区间估计中含有两个值,upper是上限,lower是下限.
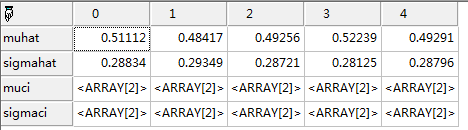
图5-3正态分布参数估计