一个指数分布的概率密度函数是：
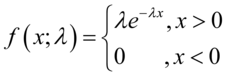            (5.13)
  其中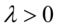是分布的一个参数，常被称为率参数.指数分布的区间是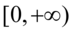. 如果一个随机变量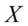呈指数分布，则可以写作.
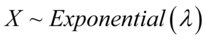  分布函数可以写成：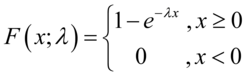
          (5.14)
  数字特征：
    ，，
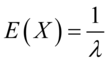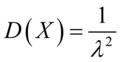  分布逆函数：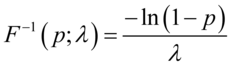
           (5.15)
  无记忆性：指数函数的一个重要特征是无记忆性，这表示如果一个随机变量呈指数分布，它的条件概率遵循：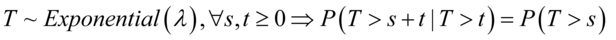
  (5.16)
  等待时间：在类似的排队论的模型中，对于强度为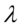的泊松质点流，等待时间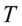服从参数为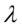的指数分布.在排队论中，无记忆性就很好理解了：在等待时间已经超过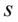的情况下，至少需要再等待时间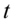的统计规律与已经等待了多少时间无关，就像重新开始等待一样.指数分布的无记忆性源于泊松分布的无记忆性.

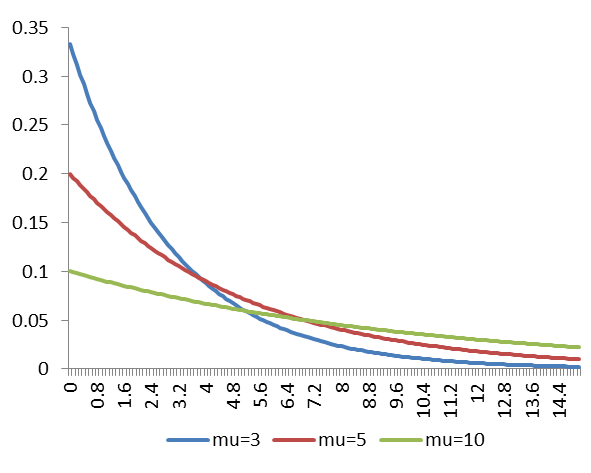
图5-13指数分布的概率密度函数
  给定独立同分布样本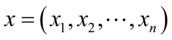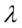，的似然函数是：
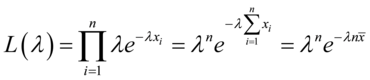      (5.17)
  率参数的最大似然估计值是：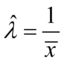
            (5.18)
相关函数：
sf_exppdf(x:array,mu:real,v:array)
sf_expcdf (x:array,mu:real,v:array)
sf_expinv (y:array,mu:real,v:array)
Randexp(mu:Real,row:Integer,col:Integer)
expfit(x:array,alpha:Real)
各参数说明：
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
mu:分布参数,实数,缺省为1
v:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
alpha:显著性水平,为0,1之间的实数,缺省为0.05
更多请参考各函数帮助说明：
sf_exppdf，sf_expcdf，sf_expinv，Randexp，expfit