若来自正态总体的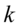个随机变量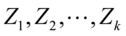相互独立，且数学期望为0、方差为1（即服从标准正态分布），则随机变量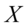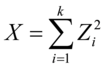（）被称为服从自由度为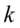的卡方分布，记作.

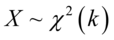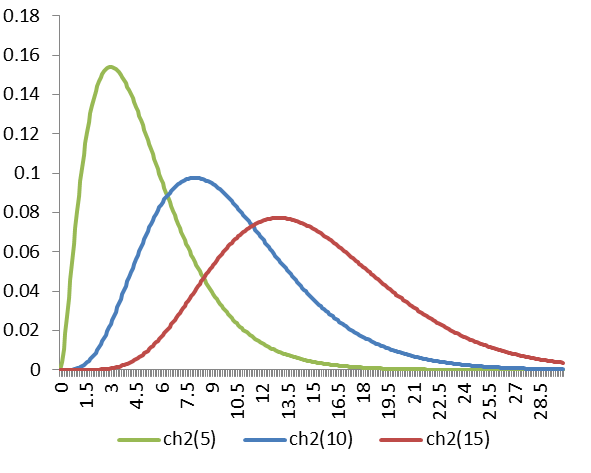
图6-16卡方分布密度函数
  概率密度函数（图5-16）：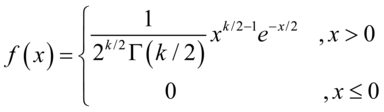
      (5.24)
  分布函数：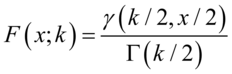
         (5.25)
其中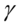为不完全Gamma函数
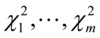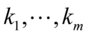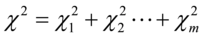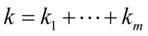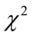  卡方分布的可加性：若相互独立，且都服从卡方分布，自由度为，则服从自由度为的分布.
  卡方分布常用于假设检验和置信区间的计算，还可以用来测试随机变量之间是否相互独立，也可用来检测统计模型是否符合实际要求.自由度为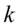的卡方变量的平均值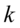是，方差是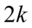. 卡方分布是伽玛分布的一个特例，它的熵为：
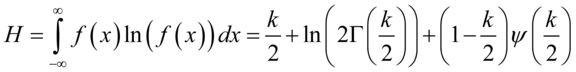   (5.26)
  其中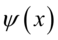是双伽玛函数.卡方变量与Gamma变量的关系是当Gamma变量频率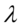为1/2时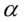，的2倍为卡方变量之自由度即:
    
    
    

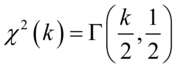
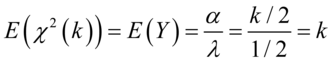
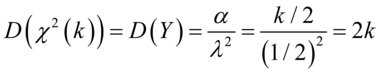
相关函数：
sf_sh2pdf(x:array,v:real,ret:array)
sf_sh2cdf(x:array,v:real,ret:array)
sf_sh2inv(y:array,v:real,ret:array)
Randsh2(v:real,row:Integer,col:Integer)
各参数说明：
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
v:卡方分布自由度,实数；
ret:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
更多请参考各函数帮助说明。