在概率论与统计学中，拉普拉斯分布是以皮埃尔-西蒙·拉普拉斯的名字命名的一种连续概率分布.由于它可以看作是两个不同位置的指数分布背靠背拼接在一起，所以它也叫作双指数分布.两个相互独立同概率分布指数随机变量之间的差别是按照指数分布的随机时间布朗运动，所以它遵循拉普拉斯分布.
  如果随机变量的概率密度函数为（如图5-24）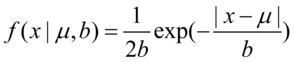
         (5.41)
  那么它就是拉普拉斯分布.记为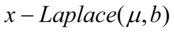：其中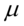，是位置参数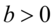，是尺度参数.

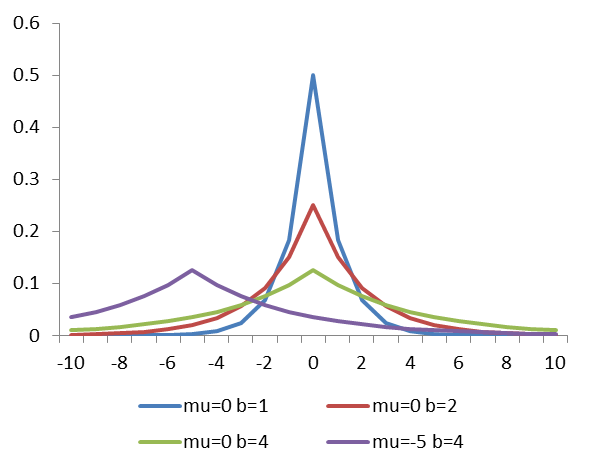
图5-24拉普拉斯分布概率密度
  它的累积分布函数为：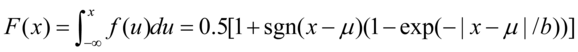
  (5.42)
  逆分布函数为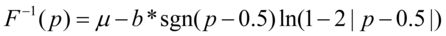
    (5.43)
  数字特征：
    ，.

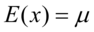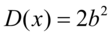相关函数：
sf_Laplacepdf (x:real,mu:real,b:real,v:real)
sf_Laplacecdf (x:real,mu:real,b:real,v:real)
sf_Laplaceinv(p:real,mu:real,b:real,v:real)
RandLaplace (mu:real,b:real,row:real,col:real)
各参数说明：
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
mu:位置参数,实数
b:尺度参数,大于0的实数
v:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
更多请参考各函数帮助说明：
sf_Laplacepdf，sf_Laplacecdf，sf_Laplaceinv，RandLaplace