柯西分布也叫作柯西-洛仑兹分布，它是以奥古斯丁·路易·柯西与亨得里柯西分布也叫作柯西-洛仑兹分布，它是以奥古斯丁·路易·柯西与亨得里克·洛仑兹名字命名的连续概率分布，其概率密度函数为
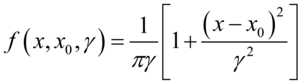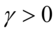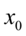，，为实数   (5.44)
  其中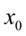是定义分布峰值位置的位置参数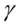，是最大值一半处的一半宽度的尺度参数.

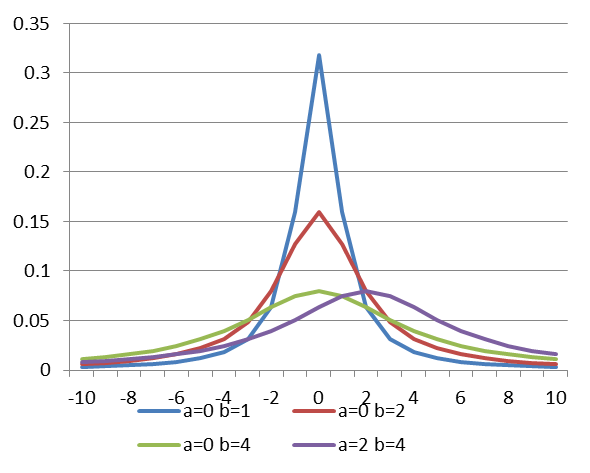
图5-25拉普拉斯分布概率密度
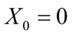  且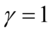的特例称为标准柯西分布，其概率密度函数为
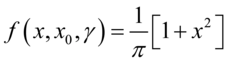          (5.45)
  特性
  其累积分布函数为：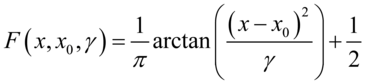
      (5.46)
  柯西分布的平均值、方差或者矩都没有定义，它的众数与中值有定义都等于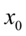

相关函数：
sf_Cauchypdf(x:real,a:real,b:real,v:real)
sf_Cauchycdf(x:real,a:real,b:real,v:real)
sf_Cauchyinv(p:real,a:real,b:real,v:real)
RandCauchy (a:real,b:real,row:real,col:real)
各参数说明：
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
a:位置参数,实数；
b:尺度参数,大于0的实数；
v:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
更多请参考各函数帮助说明。