1）经济金融理论
  凯恩斯说：通常或平均而言，人们的消费倾向于随着他们收入的增加而增加，但不如收入那么多。
2）指标的选择及回归模型的设定
  在这里，我们没有涉及指标的取舍，主要考察城镇居民消费性支出与可支配收入之间的关系。根据凯恩斯的说法，我们可以指出两者之间明确的函数关系（消费函数）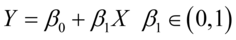

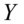  消费性支出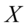，可支配收入。该方程表明消费和收入之间具有线性关系。但是一般来说，变量之间的关系是非正确的（如：除收入影响消费外，还有其他变量影响着消费支出），考虑到变量之间的非正确关系，我们把确定性的消费函数修改为

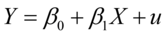
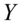  消费性支出，为被解释变量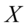，可支配收入，为解释变量。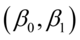为回归参数。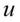为干扰项或误差项，是一个随机变量，可以用来代表所有未指明的对消费有所影响的那些因素或度量对消费的影响。
3）获取数据

表7-1：1991-2010年全国城镇家庭每人收入与消费支出数据

年份	expend	income	CPI	年份	expend	income	CPI
1991	1453.80	1700.60	223.80	2001	5309.01	6859.60	437.00
1992	1671.70	2026.60	238.10	2002	6029.92	7702.80	433.50
1993	2110.80	2577.40	273.10	2003	6510.94	8472.20	438.70
1994	2851.30	3496.20	339.00	2004	7182.10	9421.60	455.80
1995	3537.57	4282.95	396.90	2005	7942.88	10493.00	464.00
1996	3919.50	4838.90	429.90	2006	8696.55	11759.50	471.00
1997	4185.60	5160.30	441.90	2007	9997.47	13785.80	493.60
1998	4331.60	5425.10	438.40	2008	11242.85	15780.80	522.70
1999	4615.90	5854.00	432.20	2009	12264.55	17174.65	519.00
2000	4998.00	6279.98	434.00	2010	13471.45	19109.44	536.10

数据来源：中经网数据
  我们从中经网找的的数据如表7-1所列，现将这些数据描述在图7-1上。可以看出消费与收入之间确实存在着某种统计关系。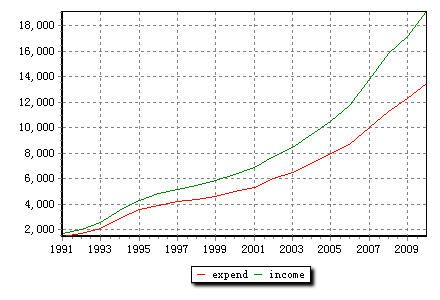

图7-1：1991-2010年城镇居民可支配收入与消费性支出间变化
4）计量经济学模型的估计
  有了数据之后，下一个任务就是估计消费函数中的参数了。
  使用Tinysoft金融分析.NET中的函数Regression函数进行参数的估计，结果如图7-3所示。
  估计结果中的Coefficient元素储存的就是参数的点估计值（如果有常数项，则排在第一位）。本例中我们得到参数的估计为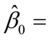538.21，。

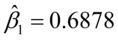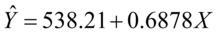
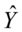  为拟合值，该回归线拟合效果如图8-2所示。

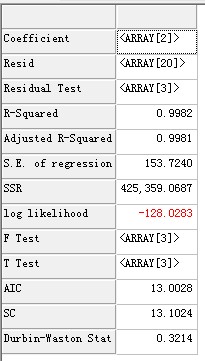
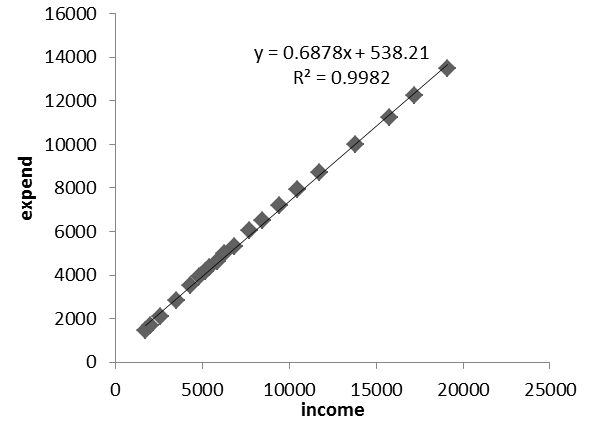图7-2 回归线拟合效果图图7-3 Tinysoft估计结果
5）假设检验
  假定所拟合的模型是现实的一个较好的近似，还必须制定适合的准则，借以判断如方程中的估计值是否和待检验的理论预期值相一致。以样本证据为依据去肯定或否定经济理论，是以所谓统计推断，以假设检验这个统计理论分支为基础。在本例中，要注意的检验有：
a) 经济意义检验：
  估计结果应该符合现实意义，是这一步检验的一个通俗的说法；
b) 模型的拟合优度检验：
i. 可决系数：估计结果中的R-Squarad元素，检验函数拟合效果。一般要求大于0.80；
ii. 修正可决系数：估计结果中的adjusted R-Squarad元素，检验内容与验证规则与R平方基本一致；
iii. AIC，SC信息准则：估计结果中的AIC，SC元素，用于在备选模型之间做出选择；
c) 回归方程的显著性检验：
i. F统计计量：估计结果中的F Test元素，检验被解释变量与解释变量之间的线性关系。这里我们可以直接看F统计量的P值，一般要求小于0.05；
ii. T统计量：估计结果中的T Test元素，检验每一个解释变对被解释变量的影响是否显著。这里我们可以直接看T统计量的P值，一般要求小于0.05；
  以上检验如有不能通过的，考虑进行模型估计的修正、模型形式的修正以及指标的更换等。
6）模型的运用（略）。