TSL语言基础 > 数学与统计教程 > 回归分析 > 多重共线性的修正
岭回归
- 岭回归分析实际上是一种改良的最小二乘法,是一种专门用于共线性数据分析的有偏估计回归方法。想法的提出也比较自然,当
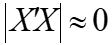 时,我们设想给
时,我们设想给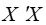 加上一个正常数矩阵
加上一个正常数矩阵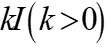 ,那么
,那么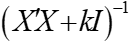 接近奇异的可能性就会比
接近奇异的可能性就会比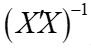 接近奇异的可能性小得多,因此用
接近奇异的可能性小得多,因此用
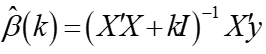 (7.29)
(7.29)
为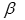 的估计应比最小二乘估计
的估计应比最小二乘估计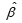 稳定,我们称(7.29)式为
稳定,我们称(7.29)式为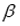 的岭回归估计,
的岭回归估计,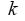 称为岭参数。显然当
称为岭参数。显然当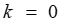 时,(3-14)就是普通的最小二乘估计。
时,(3-14)就是普通的最小二乘估计。
首先对解释变量数据进行Z分数标准化得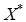 ,解方程得到的
,解方程得到的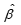 就是标准化后的解释变量对被解释变量的岭估计,其中
就是标准化后的解释变量对被解释变量的岭估计,其中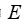 为
为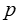 (解释变量个数)单位阵,
(解释变量个数)单位阵,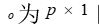 阶0向量。
阶0向量。
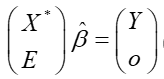 (7.30)
(7.30)
选取K值的方法有很多种,这里简单介绍两种,第一种适合用户画出岭迹图后判断,而第二种Tinysoft金融分析平台已经编程实现。
1)岭迹法:
各回归系数的岭估计基本稳定;
用最小二乘估计时符号不合理的回归系数,其岭回归的符号将变得合理;
回归系数没有不合乎经济意义的绝对值;
残差平方和增大不太多。
2)方差扩大因子法
方差扩大因子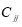 也度量了多重共线性的严重程度,我们说一般当
也度量了多重共线性的严重程度,我们说一般当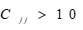 时,模型就有严重的多重共线性。
时,模型就有严重的多重共线性。
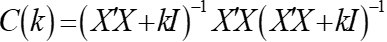 (7.31)
(7.31)
其对角元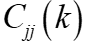 为岭估计的方差扩大因子。不难看出,
为岭估计的方差扩大因子。不难看出,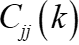 随
随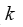 的增加而减少。应用方差因子扩大法选择
的增加而减少。应用方差因子扩大法选择的经验做法是:选择
使所有的方差扩大因子
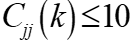 ,当
,当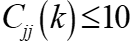 时,所对应的
时,所对应的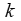 值的岭估计
值的岭估计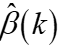 就会相对稳定。
就会相对稳定。
岭回归模型:Regress_Ridge