TSL语言基础 > 数学与统计教程 > 小波去噪

基于小波分析的金融时间序列消噪方法及应用    

  •   选取2009年4月20日~2011 年5 月19 日期间800个交易日的沪深市场沪深300日综合指数收盘价信号作为原始序列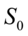(图10-1)进行去噪实验。

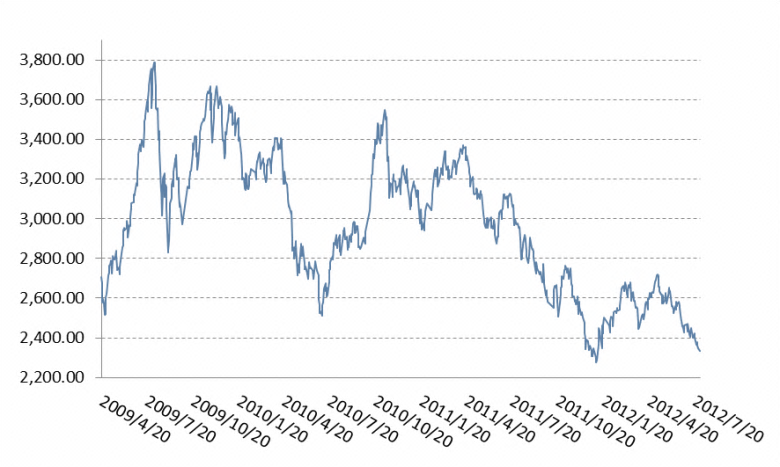
    图10-1 上证综指800个交易日收盘价数据

      根据上述理论分析,将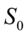进行多分辨率分解到第3层,其中采用 Daubechies 小波系的db3小波(Tinysoft现有小波如表10-1所示)和Sqtwolog阈值估计准则,进行消噪处理.分解示意图如图10-2所示,得到最后一次的低频信号，以及每次分解的高频信号.
      Ret := Wavedec(close3,3,"db3");//函数输出图10-2中的C和L.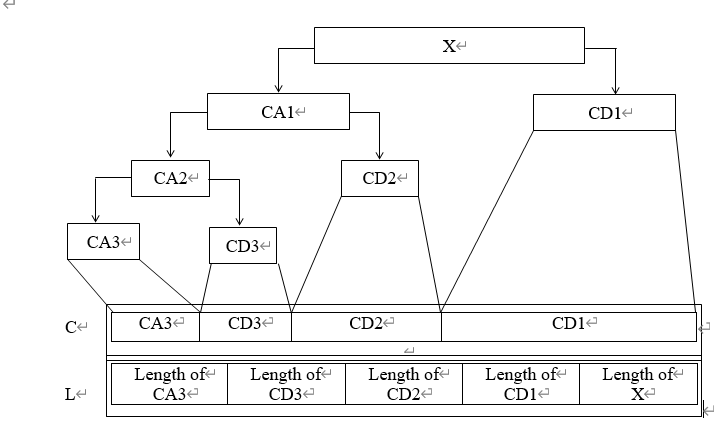

    图10-2 小波分解示意图

    图10-3wavedec函数输出结果

      第一行是小波分解向量C，第二行是相应的记录向量L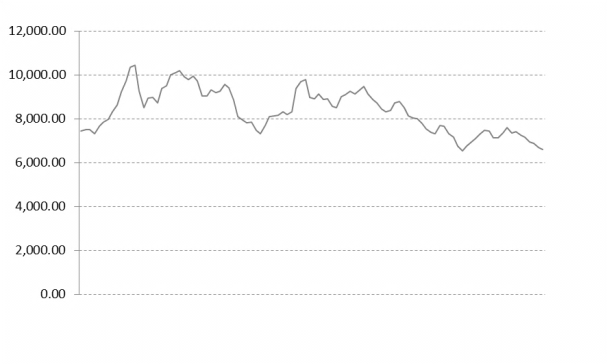


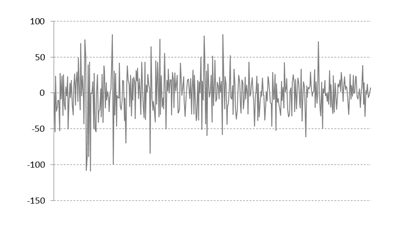
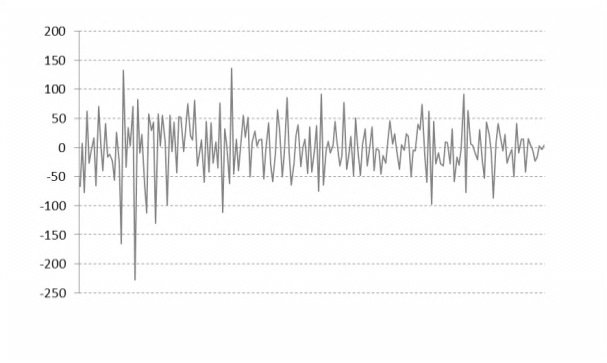
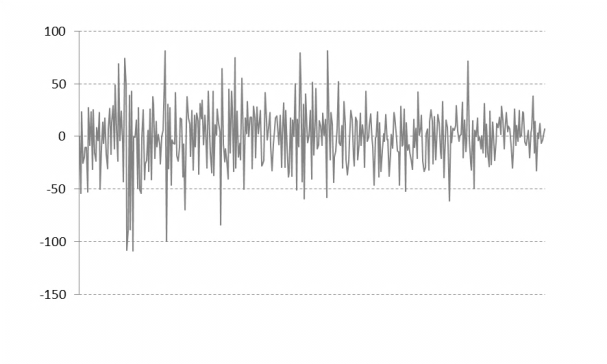
    图10-4 从左到右，从上而下分别是CA3/CD3/CD2/CD1

      然后提取CA3低频信号及根据固定阈值处理的高频信号CD1,CD2,CD3, 利用重构公式进行小波重构,就可以得到小波去噪后的序列了.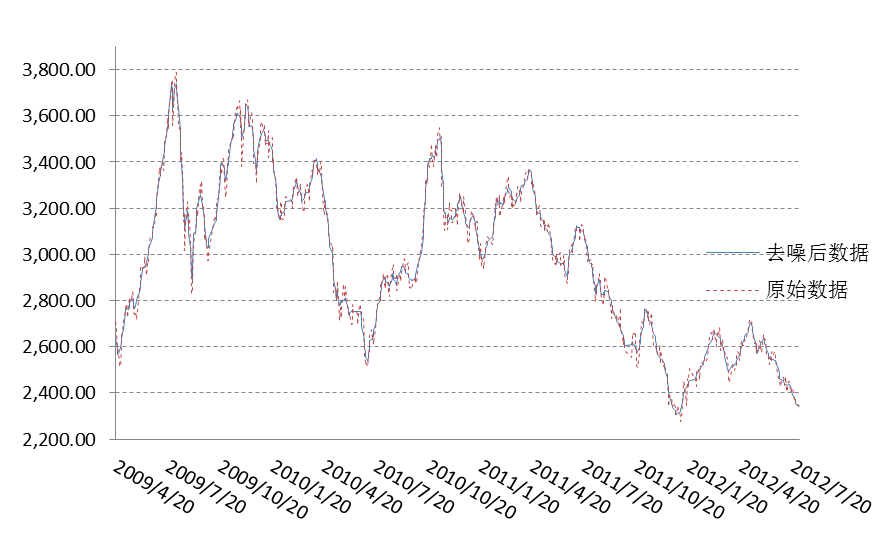

    图10-4 去噪后的数据和原始数据的对比

      将去噪后的序列与原始收盘价序列进行比较后,可以发现大部分的小幅波动被去除, 而信号的主要特征均被保留, 得到1组消噪的时间序列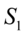.由于小幅干扰的噪声已被去除, 对于以下金融时间序列的建模可以更为方便, 而且更能反映序列的主要特征.为了验证消噪的结果, 可以将原始序列与消噪后的新序列进行时间序列的建模, 使用ARIMA模型来拟合序列,经过差分平稳化过程，观察其自相关和偏自相关分析图定阶,AIC从备选模型中选出最佳模型, 最终我选择 ARIMA(6,1,0)模型进行建模,得到相应的估计序列图分别为图10-5以及图10-6.为了更清晰的说明问题,我们得到800个完整数据在2种方法建模下的预测误差均方根值:原始序列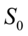建模预测方法为1764719,
    //ADF检验与差分 //return Times_ADFTest(qvzao_close3,0,0,"AIC",0,0.05);
    chafen := array();
    chafen2 := array();
    for i := 1 to length(qvzao_close3)-1 do
    chafen[i-1] := qvzao_close3[i]-qvzao_close3[i-1];
    //return Times_ADFTest(chafen,0,0,"AIC",0,0.05);
    for i := 1 to length(qvzao_close3)-1 do
    chafen2[i-1] := close3[i]-close3[i-1];
    //中心化
    a := mean(chafen);
    a2 := mean(chafen2);
    chafen := chafen -a;
    chafen2 := chafen2 -a2;
    //拟合AR模型
    coff := -ARMA(chafen,6,0)["AR"][1:];
    coff2 := -ARMA(chafen2,6,0)["AR"][1:];
    coff := coff[array(5,-1)->0];
    coff2 := coff2[array(5,-1)->0];
    //差分序列预测
    chafen_fore := chafen;
    chafen_fore2 := chafen2;
    for i:=6 to length(chafen)-1 do
    begin
    chafen_fore[i] := sum(coff*chafen[(i-6):(i-1)]);
    chafen_fore2[i] := sum(coff2*chafen2[(i-6):(i-1)]);
    end
    chafen_fore += a;
    chafen_fore2 += a2;
    //收盘价序列预测
    close_fore := qvzao_close3;
    close_fore2 := close3;
    for i:=1 to length(close3)-1 do
    begin
    close_fore[i] := qvzao_close3[i-1]+chafen_fore[i-1];
    close_fore2[i] := close3[i-1]+chafen_fore2[i-1];
    end
    //比较两者的残差平方和
    return array(sum((close_fore-close3)^2),sum((close_fore2-close3)^2));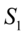
      消噪序列建模预测误差平方和为1065984，不去除噪声拟合预测的误差平方和是1764719。从中可以看出,用消噪后的信号进行建模预测得到的估计值误差更小,也更能反映原始信号的波动情形,而如果不做处理直接进行建模,那么在预测的序列中增加了许多随机干扰,也就是随机误差比较多,这样会影响预测的结果.

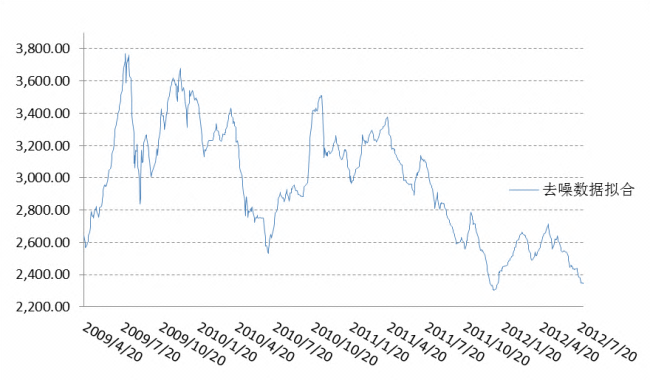
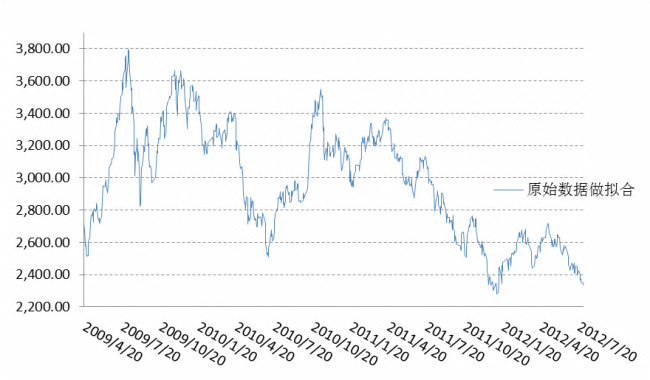
    图10-5 去噪数据估计模型的预测序列图10-6原始数据估计模型的预测序列

    最后在补充个一维离散小波单支重构的函数：wrcoef
内容