TSL语言基础 > 数学与统计教程 > 多元统计分析 > 判别分析
Fisher判别
- Fisher判别的基本思想是投影,将
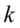 组m维数据投影到一个方向,使得投影后组和组之间尽可能地分开,而衡量组和组之间之间是否分开的方法借组于一元方差分析的思想.
组m维数据投影到一个方向,使得投影后组和组之间尽可能地分开,而衡量组和组之间之间是否分开的方法借组于一元方差分析的思想.
设p维总体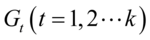 ,
,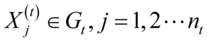 ,令
,令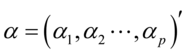 为
为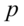 维空间中任一向量,
维空间中任一向量,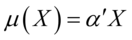 表示
表示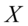 在方向
在方向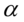 上的投影,通过这样的投影,我们把数据转化为
上的投影,通过这样的投影,我们把数据转化为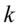 组数据:
组数据: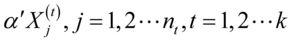 ,按方差分析的思想,其组间平方和为
,按方差分析的思想,其组间平方和为
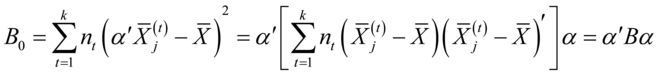 (4-17)
(4-17)
合并的组内平方和:
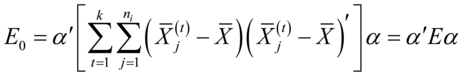 (4-18)
(4-18)
其中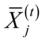 ,
,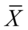 分别是
分别是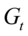 的样本均值以及总样本均值。若
的样本均值以及总样本均值。若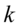 类的均值有显著差异,则比值
类的均值有显著差异,则比值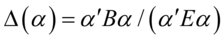 应该充分大.因为该值也被
应该充分大.因为该值也被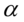 的量纲影响,因此我们加入约束条件:
的量纲影响,因此我们加入约束条件: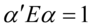 ,这样,我们就只需要找
,这样,我们就只需要找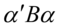 的极大值.
的极大值.
使用lagrange乘数法可以容易地导出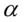 为特征方程
为特征方程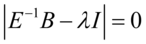 的最大特征跟对应的满足
的最大特征跟对应的满足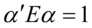 的特征向量.如果使用一个线性特征方程不能很好的区分各个总体,则可使用第二、第三特征向量.
的特征向量.如果使用一个线性特征方程不能很好的区分各个总体,则可使用第二、第三特征向量.
判别模型:Discrim