天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 多元统计分析
corr_canonical
简述
典型相关分析,默认条件从中心化数据出发衡量两组随机变量之间的相关性定义
corr_canonical(x:Array;y:Array;alpha:Float;Standarize_choice:Integer):Array;
参数
| 名称 | 类型 | 说明 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | Array | X属性样本数据,二维数字数组,详见实例分析 | ||||||||||||||||
| y | Array | Y属性样本数据,二维数字数组,详见实例分析 | ||||||||||||||||
| alpha | Float | 置信度,实数型,0~1之间,缺省值0(不执行典型相关系数显著性检验) | ||||||||||||||||
| Standarize_choice | Integer | 原始数据标准化选择,整数型,0~7,缺省值为0(保持原始数据)
| ||||||||||||||||
| 返回 | Array | 二维数组。结果说明:
ret["cor",0]:典型相关系数 ret["xcoef",0]:随机变量组X的线性组合系数 ret["ycoef",0]:随机变量组Y的线性组合系数 ret["xcenter",0]:X向量的中心,即X向量的样本均值 ret["ycenter",0]:Y向量的中心,即Y向量的样本均值 ret["典型相关系数相关性检验",0]:返回有效相关系数对数,为0则不需要做该分析 |
- 算法
典型性分析算法说明:
典型相关分析是用来分析两组随机变量之间的相关性程度的一种统计方法,它能够有效地解释两组随机变量之间相互线性依赖的关系。
比如在实际问题中,经常遇到一部分变量和另一部分变量之间的相互关系。例如,在经济学中研究商品价格的相关指标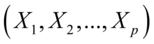 和销售的相关指标
和销售的相关指标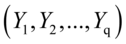 之间的关系;在地质学中,研究岩石形成的成因关系,考察岩石的化学成分与其周围化学成分的相关性;教育学中,考察学生入学考试成绩和本科阶段一些主要课程成绩的相关性;在统计学中,也可以用来做随机变量之间的多重共线性判断和重构随机变量组,改进随机变量之间多重共线性问题,使得回归分析等结果更加合理,等等。
之间的关系;在地质学中,研究岩石形成的成因关系,考察岩石的化学成分与其周围化学成分的相关性;教育学中,考察学生入学考试成绩和本科阶段一些主要课程成绩的相关性;在统计学中,也可以用来做随机变量之间的多重共线性判断和重构随机变量组,改进随机变量之间多重共线性问题,使得回归分析等结果更加合理,等等。
一般地,假设有两组随机变量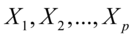 和
和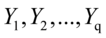 研究它们的相关关系,当p=q=1时,就是通常两个随机变量之间的相关关系;当p>1,q>1时,采用类似主成分分析的方法,找出
研究它们的相关关系,当p=q=1时,就是通常两个随机变量之间的相关关系;当p>1,q>1时,采用类似主成分分析的方法,找出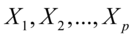 的线性组合U和
的线性组合U和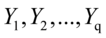 的线性组合V,即:U=
的线性组合V,即:U=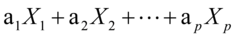 ,
,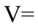
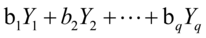 ,于是将研究两组变量的相关性问题转化成研究两个变量的相关性问题,并且可以适当的调整系数a 和b,使得U和V的相关性达到最大,称这种相关为典型相关,基于这种原则的分析方法称为典型相关分析。
,于是将研究两组变量的相关性问题转化成研究两个变量的相关性问题,并且可以适当的调整系数a 和b,使得U和V的相关性达到最大,称这种相关为典型相关,基于这种原则的分析方法称为典型相关分析。
第一步,先定义典型相关,设X=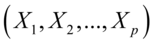 和Y=
和Y=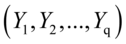 为随机向量,用X和Y的线性组合
为随机向量,用X和Y的线性组合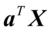 和
和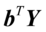 之间相关性来研究X与Y之间的相关性,并希望找到a与b,使得
之间相关性来研究X与Y之间的相关性,并希望找到a与b,使得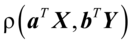 最大。由相关系数定义,
最大。由相关系数定义,
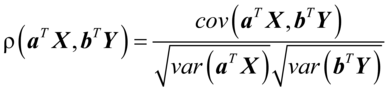
(4. 1)
对任意的α,β和c,d有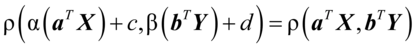
(4. 2)
式(4.2)说明,使得相关系数最大的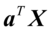 和
和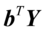 并不唯一。因此,在综合变量,可限定
并不唯一。因此,在综合变量,可限定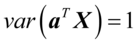 ,
,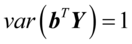 。
。
总结一下第一步,设X=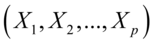 和Y=
和Y=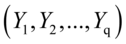 ,p+q维随机向量
,p+q维随机向量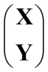 的均值为0,协方差阵正定。若存在a1=
的均值为0,协方差阵正定。若存在a1=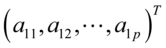 和b1=
和b1=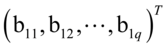 ,使得
,使得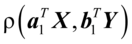 是约束问题
是约束问题
max 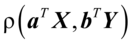
(4. 3) s.t. 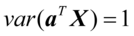
(4. 4) 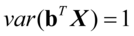
(4. 5)
目标函数的最大值,则成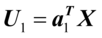 ,
,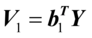 为
为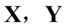 的第一对典型变量,称它们之间的相关系数
的第一对典型变量,称它们之间的相关系数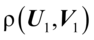 为第一典型相关系数。
为第一典型相关系数。
如果存在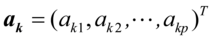 和
和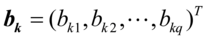 使得
使得
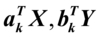 和前面的k-1对典型变量都不相关;
和前面的k-1对典型变量都不相关;
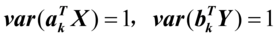 ;
;
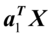 和
和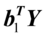 相关系数最大
相关系数最大
则称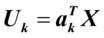 ,
,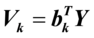 为
为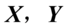 的第k对典型变量,称它们之间的相关系数
的第k对典型变量,称它们之间的相关系数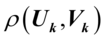 为第k典型相关系数
为第k典型相关系数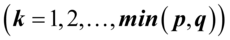 典型相关系数。
典型相关系数。
第二步,下面直接给出计算过程所需的重要推导步骤以及计算过程:
设Z=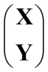 ,则有
,则有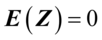 ,
,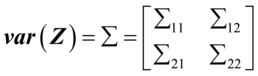 ,令
,令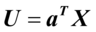 ,
,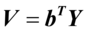 ,因此,求解第一对典型变量和典型相关系数的约束问题式(4.3)~(4.5)就等价为
,因此,求解第一对典型变量和典型相关系数的约束问题式(4.3)~(4.5)就等价为
max 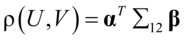
(4. 6) s.t. 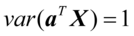
(4. 7) 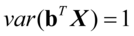
(4. 8)
这是一个典型的约束优化问题,这里采用拉格朗日乘数法求解该约束问题,其中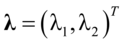 为Lagrange乘子,得到如下方程:
为Lagrange乘子,得到如下方程:
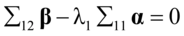
(4. 9) 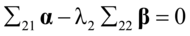
(4. 10) 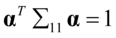
(4. 11) 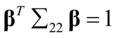
(4. 12)
求解上述方程组,在式(4.6)左乘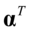 ,在式(4.7)左乘
,在式(4.7)左乘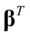 ,然后将式(4.8)代入式(4.6),将式(4.9)代入式(4.7),得到结果
,然后将式(4.8)代入式(4.6),将式(4.9)代入式(4.7),得到结果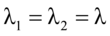 。由于
。由于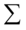 正定(在第一步中有定义,即使没有定义的情况下协方差矩阵也是半正定的),所以
正定(在第一步中有定义,即使没有定义的情况下协方差矩阵也是半正定的),所以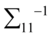 和
和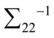 存在,先将式(4.6)和(4.7)中
存在,先将式(4.6)和(4.7)中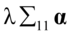 和
和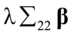 移到等号右边,然后再分别左乘
移到等号右边,然后再分别左乘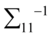 和
和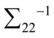 ,得到
,得到
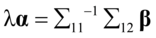 ,
,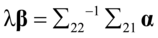
(4. 13)
然后将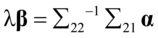 代入
代入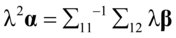 式中,所以有
式中,所以有
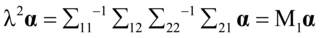
(4. 14)
同理,可得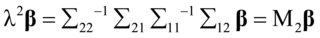
(4. 15)
其中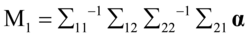 ,
,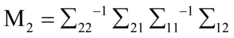 。
。
因此,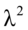 是矩阵
是矩阵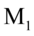 特征根(注意,
特征根(注意,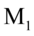 和
和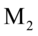 具有相同的特征根),
具有相同的特征根),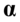 是
是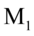 的特征根对应的特征向量,
的特征根对应的特征向量,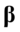 是
是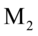 的特征根对应的特征向量。
的特征根对应的特征向量。
由于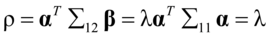 ,式(4.9)和式(4.11)可得。所以典型相关系数
,式(4.9)和式(4.11)可得。所以典型相关系数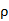 就是
就是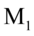 和
和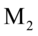 共有根号下的特征根。
共有根号下的特征根。
因此,优化问题式(4.3)~式(4.5)的解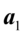 和
和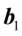 就是求
就是求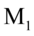 或
或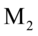 最大特征跟
最大特征跟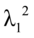 相应的特征向量
相应的特征向量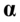 和
和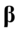 。
。
计算步骤如下:
令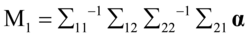 ;
;
计算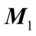 最大的特征根
最大的特征根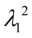 和对应的特征向量
和对应的特征向量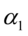 ,令
,令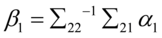 ,
,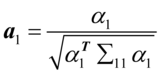 ,
,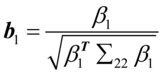 ,则
,则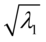 为第一对典型相关系数,
为第一对典型相关系数,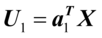 ,
,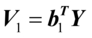 为第一对典型变量。
为第一对典型变量。
对于第k对典型变量的求解方法类似于第一对典型相关变量,只需要将(2)改为
计算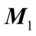 最大的特征根
最大的特征根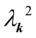 和对应的特征向量
和对应的特征向量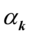 ,令
,令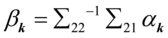 ,
,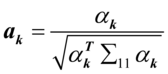 ,
,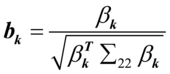 ,则
,则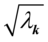 是第k对典型相关系数,
是第k对典型相关系数,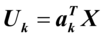 ,
,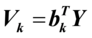 为第k对典型变量。
为第k对典型变量。
第三步,由于在实际中,设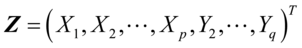 ,
,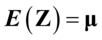 和
和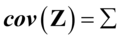 ,所以无法求出典型变量和典型相关系数,需要用样本数据估计样本协方差矩阵
,所以无法求出典型变量和典型相关系数,需要用样本数据估计样本协方差矩阵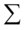 。
。
已知,总体Z的n次观测数据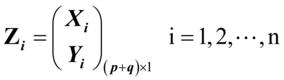
于是可给出Z的样本资料矩阵为
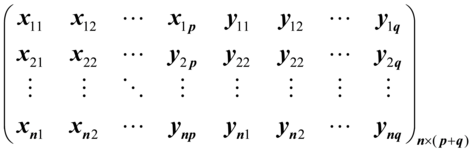
假设Z~Np+q(μ,∑),则样本协方差的极大似然估计为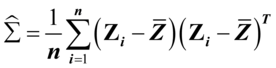
其中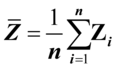 ,称
,称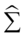 为样本协方差矩阵。具体计算过程和第二步中的计算步骤基本相同,只需要将
为样本协方差矩阵。具体计算过程和第二步中的计算步骤基本相同,只需要将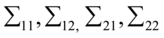 替换为
替换为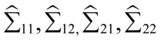 即可求解。范例
即可求解。范例
实例1:
某康复俱乐部对两组指标的典型相关性分析
某康复俱乐部对20名中年人测量了3个生理指标:体重(X1)、腰围(X2)、脉搏(X3)和三个训练指标:引体向上(Y1)、仰卧起坐次数(Y2)、跳跃次数(Y3)
表1 :某康复俱乐部两组生理指标的典型相关分析编号 X1 X2 X3 Y1 Y2 Y3 1 191 36 50 5 162 60 2 193 38 58 12 101 101 3 189 35 46 13 155 58 4 211 38 56 8 101 38 5 176 31 74 15 200 40 6 169 34 50 17 120 38 7 154 34 64 14 215 105 8 193 36 46 6 70 31 9 176 37 54 4 60 25 10 156 33 54 15 225 73 11 189 37 52 2 110 60 12 162 35 62 12 105 37 13 182 36 56 4 101 42 14 167 34 60 6 125 40 15 154 33 56 17 251 250 16 166 33 52 13 210 115 17 247 46 50 1 50 50 18 202 37 62 12 210 120 19 157 32 52 11 230 80 20 138 33 68 2 110 43
return corr_canonical(x,y,0.1,1);
实例2:企业经济效益典型相关分析
某市为了全面分析机械类各企业的经济效益,选择了8个不同的利润指标,14家企业关于这8个指标的统计数据如表4-1所示.
表2:机械类各企业的经济效益主成分分析企业 X1净产值利润率% X2固定资产利润率% X3总产值利润% X4销售收入利润率% Y1产品成本利润率% Y2物耗利润率% Y3人均利润率千元/人 Y4流动资金利润率% 1 40.4 24.7 7.2 6.1 8.3 8.7 2.44 20.0 2 25.0 12.7 11.2 11.0 12.9 20.2 3.542 9.1 3 13.2 3.3 3.9 4.3 4.4 5.5 0.578 3.6 4 22.3 6.7 5.6 3.7 6.0 7.4 0.176 7.3 5 34.3 11.8 7.1 7.1 8.0 8.9 1.726 27.5 6 35.6 12.5 16.4 16.7 22.8 29.3 3.017 26.6 7 22.0 7.8 9.9 10.2 12.6 17.6 0.847 10.6 8 48.4 13.4 10.9 9.9 10.9 13.9 1.772 17.8 9 40.6 19.1 19.8 19.0 29.7 39.6 2.449 35.8 10 24.8 8.0 9.8 8.9 11.9 16.2 0.789 13.7 11 12.5 9.7 4.2 4.2 4.6 6.5 0.874 3.9 12 1.8 0.6 0.7 0.7 0.8 1.1 0.056 1.0 13 32.3 13.9 9.4 8.3 9.8 13.3 2.126 17.1 14 38.5 9.1 11.3 9.5 12.2 16.4 1.327 11.6 //首先选取数据并且对数据做标准化z-score,消除量纲对结果的影响
X:=data[:][0:3];
Y:=data[:][4:7];
returncorr_canonical(X,Y,0.1,1);
数据返回结论分析:
首先说明XCenter和YCenter返回结果都为零是因为做了数据标准化的结果。从Cor我们可以看出X和Y这两组随机变量之间具有很高的相似度,第一对典型相关系数达到100%的相似度。在这里想说明的是,如果在对类似数据进行回归分析的时候,回归诊断发现了比较严重的多重共线性的时候,此时可以运用典型相关分析的方法,提取出典型相关成都最高的第一对典型相关组合U或者V来代替之前出现多重共线性的随机变量,从而消除和改进回归模型的病态和精度。
相关