正态分布又名高斯分布，若随机变量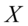服从一个位置参数为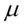、尺度参数为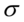的概率分布，记为：
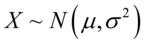           (5.18)
  则其概率密度函数为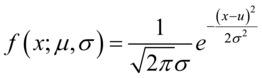
        (5.19)
  正态分布的数学期望值或期望值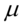等于位置参数，决定了分布的位置；其方差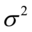的开平方或标准差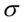等于尺度参数，决定了分布的幅度.
  正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是位置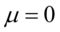参数，尺度参数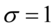的正态分布.（如图5-14）
  函数曲线下68.27%的面积在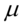左右的一个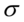范围内，95.45%的面积在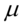左右两个标准差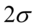的范围内，99.73%的面积在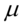左右三个标准差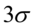的范围内.99.99%的面积在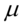左右四个标准差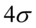的范围内（如图5-15）.
  
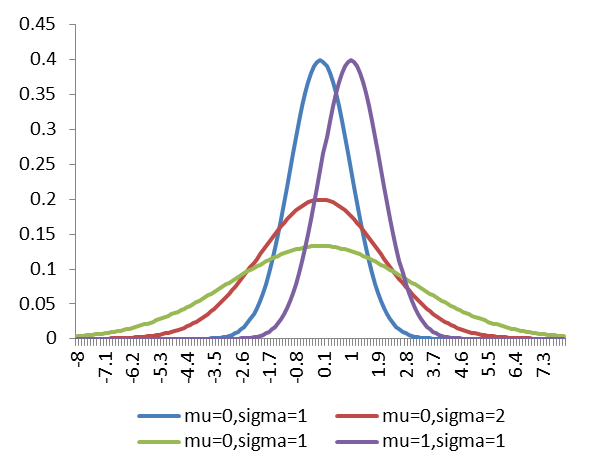
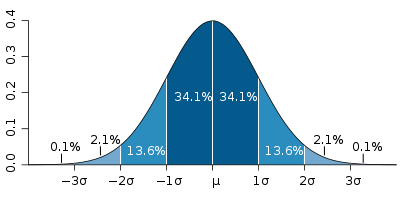
图5-14 正态分布密度概率函数图5-15 正态分布数据分布状况
  正态分布的累积分布函数可以表示为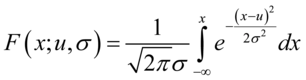
         (5.20)
  正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示：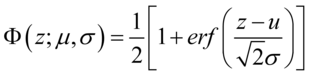
        (5.21)
  标准正态分布的累积分布函数习惯上记为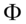，它仅仅是指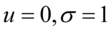时的值.
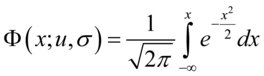          (5.21)
  将一般正态分布用误差函数表示的公式简化，可得：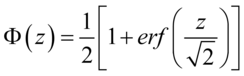
         (5.22)
  它的反函数被称为反误差函数，为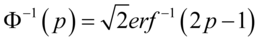
        (5.23)
  该分位数函数有时也被称为probit函数.probit函数已被证明没有初等原函数.正态分布的分布函数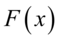没有解析表达式，它的值可以通过数值积分、泰勒级数或者渐进序列近似得到.
中心极限定理：在特定条件下，大量统计独立的随机变量的平均值的分布趋于正态分布，这就是中心极限定理.中心极限定理的重要意义在于，根据这一定理的结论，其他概率分布可以用正态分布作为近似.
  正态分布的一些性质:
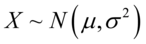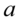  1）如果且与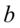是实数，那么，.
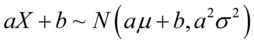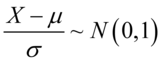  2）如果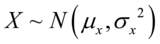与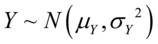是统计独立的正态随机变量，那么它们的和也满足正态分布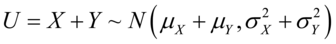，它们的差也满足正态分布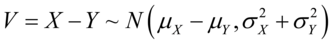.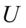和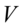是相互独立的.
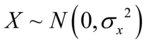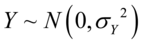  3）如果与是独立正态随机变量，那么:它们的积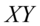服从概率密度函数为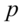的分布

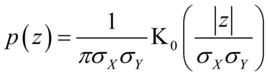
  其中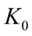是修正贝塞尔函数，它们的比符合柯西分布，满足

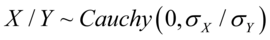
  4）如果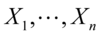为独立标准正态随机变量，那么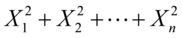服从自由度为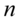的卡方分布.
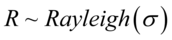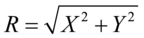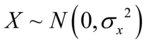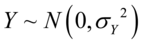  5）是瑞利分布，如果，与是独立正态随机变量.
  6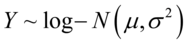）是对数正态分布，如果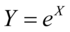并且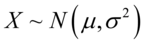

相关函数：
sf_normpdf(x:array,mu:real,sigma:real,v:array)
sf_normcdf (x:array,mu:real,sigma:real,v:array)
sf_norminv (y:array,mu:real,sigma:real,v:array)
Randnorm(mu:real,sigma:real,row:Integer,col:Integer)
normfit(x:array,alpha:Real);
各参数说明：
x:随机变量 ,实数,一位数字数组,二维数字数组
y:分布函数值,实数,一维数字数组,二维数字数组
mu:正态分布位置参数,实数,缺省为0
sigma：正态分布尺度参数,缺省为1
v:返回变参,概率或累计概率或随机变量,维度和函数第一个变量一致
row:行数,也可以是行名数组
col:列数,也可以是列名数组
alpha:显著性水平,为0,1之间的实数,缺省为0.05

更多请参考各函数帮助说明：
sf_normpdf，sf_normcdf，sf_norminv，Randnorm，Normfit