天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 统计分布

sf_normcdf    

简述
计算随机变量在正态分布, 均值为mu，方差为sigma条件下的分布函数,返回分布函数值。
定义
sf_normcdf(x:Real or Array of Real;mu:Real;sigma:Real;var v:Real or Array of Real)
参数
名称类型说明
xReal or Array of Real:随机变量，可以是实数，也可以是一个实数二维数组
muReal正态分布的均值，实数类型
sigmaReal正态分布的标准差，大于0的实数
vReal or Array of Real变参返回x对应的正态分布函数的值，实数或二维数组
  • 算法

    标准正态分布的概率密度函数为：
    pt=12πe-t22      t∈(-∞,+∞)
    则随机变量x对应分布函数(x)：
    (x)=12π-∞xe-t22dt
    定义函数erfx=2π0xe-t2dt(x>0)为误差函数；
    函数erfcx=1-erfx=2πx+∞e-t2dt为余误差函数。
    则分布函数x与余误差函数有以下关系：
    x=0.5*erfc(-x2)
    设随机变量服从均值为mu，标准差为sigma的正态分布Nmu,sigma，经过标准化
    z=x-musigma
    后服从标准正态分布N0,1。
    变量z对应的分布函数值为：
    z=0.5*erfc(-z2)
    范例

    x := array(-4,0.1)->4;
    return sf_normcdf(x,0,1);

    结果：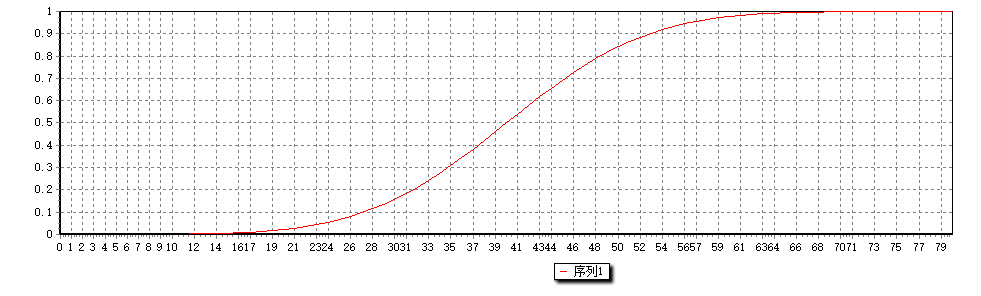
    参考
    分布函数 sf_normpdf sf_norminv Randnorm Normfit 
相关