TSL语言基础 > 数学与统计教程 > 回归分析
多元线性回归
- 7.1节中的例子只是一个简单的单变量线性回归模型,下面我们介绍下更具一般性的多元线性回归模型的理论.
多元线性回归的一般形式是(7.1)
多元总体回归函数: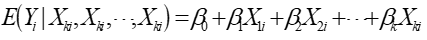 (7.2)
(7.2)
式7-2被称为调节期望函数(CEF)或总体回归函数(PRF)。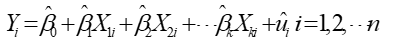 (7.3)
(7.3)
式7-3可以被叫做样本回归方程(SRF)。是根据所选样本估算的总体被解释变量和解释变量之间的回归关系。
对于7-1形式的多元线性回归模型,我们还可以使用矩阵来简化:(7.1)
其中: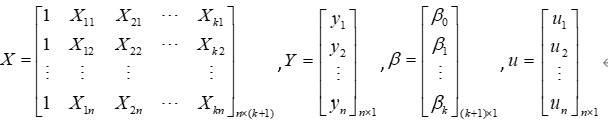
模型7-1及7-3在满足多元线性回归模型的基本假设的情况下,可以采用普通最小二乘法或最大似然估计法估计出参数。这五个经典假设分别是:
1)解释变量是非随机的,即重复抽样中,解释变量取固定值,且相互之间互不相关,无多重共线;
2)随机干扰项与解释变量之间不相关;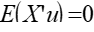
3)随机干扰项服从零均值、同方差、零协方差
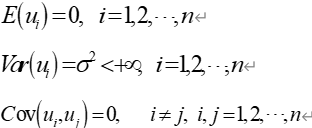
4)随机干扰项服从正态分布,即
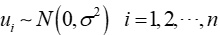
5)正确设定回归模型,含三点:
>>选择正确的变量进入模型;
>>对模型的形式进行正确的设定;
>>对模型的解释变量,被解释变量以及随机干扰项做出正确的假定。
多元线性回归的估计方法一般包含以下两种:
1)普通最小二乘法
使残差平方和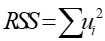 达到最小。
达到最小。
这里,我们使用RSS对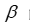 中的每一个元素求偏导,并都令为0,就可以得到正规方程组。
中的每一个元素求偏导,并都令为0,就可以得到正规方程组。
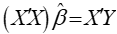 (7.4)
(7.4)
如果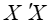 满秩,秩为
满秩,秩为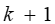 ,我们可以得到参数的估计:
,我们可以得到参数的估计: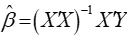 。
。
随机干扰项的方差的无偏估计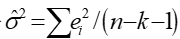 。
。
2)极大似然法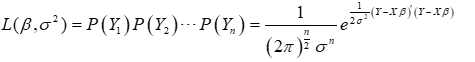 (7.5)
(7.5)
式7-5是极大似然函数,求得的最终结果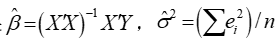 。
。
普通最小二乘法和极大似然法估计出来的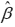 是一样的,如果方程满足经典假设,该估计值具有线性性,无偏性,最小方差性。普通最小二乘法估计出来的
是一样的,如果方程满足经典假设,该估计值具有线性性,无偏性,最小方差性。普通最小二乘法估计出来的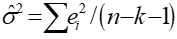 是
是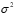 的无偏估计量。
的无偏估计量。
回归方程的最小二乘法参数估计模型:Regress_CMLS
多元线性回归模型的统计检验
多元线性回归函数模型的参数估计出来以后,需要进一步的对样本回归函数进行检验,以判断估计的可靠性。
1.模型拟合优度检验
1)可决系数
总离差的分解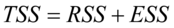 ,其中
,其中
总离差平方和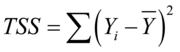 ,其中
,其中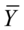 为被解释变量
为被解释变量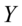 的均值;
的均值;
残差平方和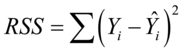 ,其中
,其中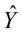 为被解释变量
为被解释变量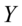 根据回归方程得到的估计值;
根据回归方程得到的估计值;
回归平方和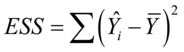 ,其中
,其中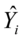 ,
,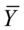 分别是被解释变量估计值和均值。
分别是被解释变量估计值和均值。
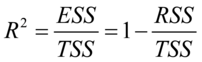 (7.6)
(7.6)
式(2-6)给出了样本可决系数的定义,该统计量是描述拟合优度的一个重要的指标。由定义,我们知道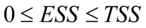 ,所以一般的
,所以一般的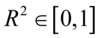 ,
,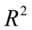 越接近于1,表明残差平方和越小,样本回归线和样本观测值的拟合程度越高。
越接近于1,表明残差平方和越小,样本回归线和样本观测值的拟合程度越高。
将残差平方和与总离差平方和之比的分子分母分别使用他们各自的自由度去除,变成均方差之比,以消除解释变量个数对可决系数的影响,修正的样本决定系数为: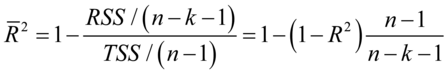 (7.7)
(7.7)
2)AIC,SC信息准则这两个指标被使用来比较所含解释变量个数不同的多元回归模型的拟合集成度。
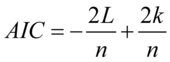 (7.8)
(7.8)
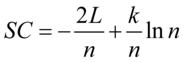 (7.9)
(7.9)
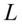 为对数似然值,
为对数似然值,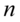 为观测数目,
为观测数目,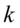 为被估计的参数个数。信息准则和修正的样本可决系数类似,在评价模型优劣时兼顾了简洁性和精确性。这两个指标都是越小越好。这两个准则要求仅当所增加的解释变量能够减少AIC,SC统计量,才能在原模型中增加该解释变量。
为被估计的参数个数。信息准则和修正的样本可决系数类似,在评价模型优劣时兼顾了简洁性和精确性。这两个指标都是越小越好。这两个准则要求仅当所增加的解释变量能够减少AIC,SC统计量,才能在原模型中增加该解释变量。
2.回归方程的显著性检验
原假设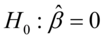 ,备选假设
,备选假设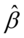 不全为0。
不全为0。
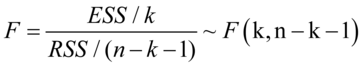 (7.10)
(7.10)
如果发生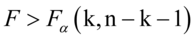 ,则在
,则在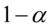 水平下拒绝原假设,即模型的线性关系显著成立,模型通过方程显著性检验。
水平下拒绝原假设,即模型的线性关系显著成立,模型通过方程显著性检验。
如果发生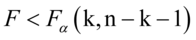 ,则在
,则在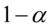 水平下接受原假设,即模型的线性关系显著不成立,模型不通过方程显著性检验。
水平下接受原假设,即模型的线性关系显著不成立,模型不通过方程显著性检验。
与修正样本可决系数之间的关系: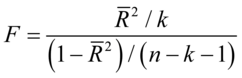
上式表明,这两个统计量同向变化,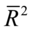 =0时,
=0时,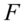 =0;
=0;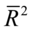 越大,
越大,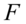 越大;
越大;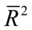 =1时,
=1时,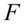 无穷大。因此,F检验可用于度量总体回归线的显著性检验,也可以检验
无穷大。因此,F检验可用于度量总体回归线的显著性检验,也可以检验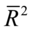 的显著性。
的显著性。
3.变量的显著性检验
检验模型的解释变量是否对被解释变量有显著影响的假设检验。原假设: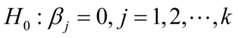 ,备选假设:
,备选假设: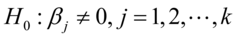
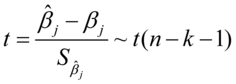 (7.11)
(7.11)
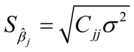 ,
,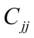 为
为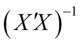 对角线上的第j+1个元素,
对角线上的第j+1个元素,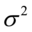 使用
使用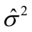 。
。
若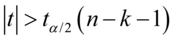 则在
则在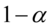 水平下拒绝原假设 ,即
水平下拒绝原假设 ,即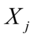 对应的解释变量
对应的解释变量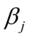 是显著的;
是显著的;
若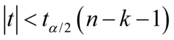 ,则在
,则在 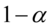 水平下拒绝原假设,即
水平下拒绝原假设,即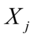 对应的解释变量
对应的解释变量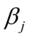 是不显著的。
是不显著的。
4.随机序列的正态性JB检验
检验一个随机序列是否服从正态分布。原假设:该随机序列为正态分布,备选假设:该随机序列不为正态分布,我们有统计量: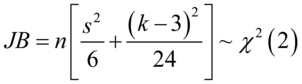 (7.12)
(7.12)
其中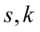 分别为随机序列的偏度和峰度
分别为随机序列的偏度和峰度
若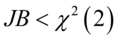 则在
则在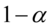 水平下拒绝原假设,即随机序列不为正态分布;
水平下拒绝原假设,即随机序列不为正态分布;
若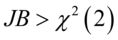 则在
则在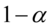 水平下接受原假设,即随机序列为正态分布。
水平下接受原假设,即随机序列为正态分布。
5.多元线性回归模型的置信区间
参数估计量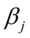 的置信水平
的置信水平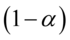 的置信区间为:
的置信区间为:
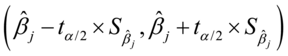 (7.13)
(7.13)
参数估计量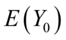 的置信水平
的置信水平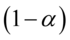 的置信区间为:
的置信区间为:
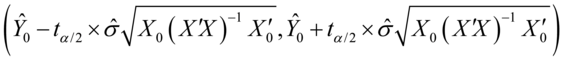 (7.14)
(7.14)
参数估计量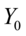 的置信水平
的置信水平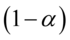 的置信区间为:
的置信区间为:
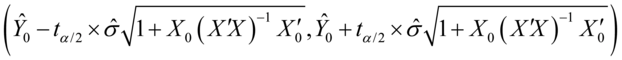 (7.15)
(7.15)
对多元线性回归模型进行估计及假设检验模型:Regression