TSL语言基础 > 数学与统计教程 > 时间序列分析 > ARMA模型

平稳性检验    

  •   
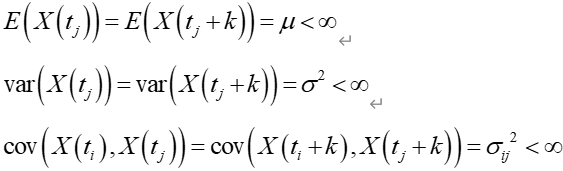
      其中为二阶平稳时间序列(协方差平稳时间序列)。这也就是我们常说的平稳时间序列，我们也可以叫他宽平稳过程。
    检验方法：
    1)时序图
      取上证综指2011年9月1日到2012年8月7日共计225个交易日的数据.
      SetSysParam(pn_stock(),"SH000001");
      SetSysParam(PN_Date(),inttodate(20120807));
      N := tradedays(inttodate(20110901),inttodate(20120807));
      close1 := nday(N,"time",datetostr(sp_time()),"close",close());
      //时间以及对应的收盘价
      clos := close1[:,"close"]; //收盘价
      dclose := clos[1:]-clos[0:length(clos)-2]; //差分
      


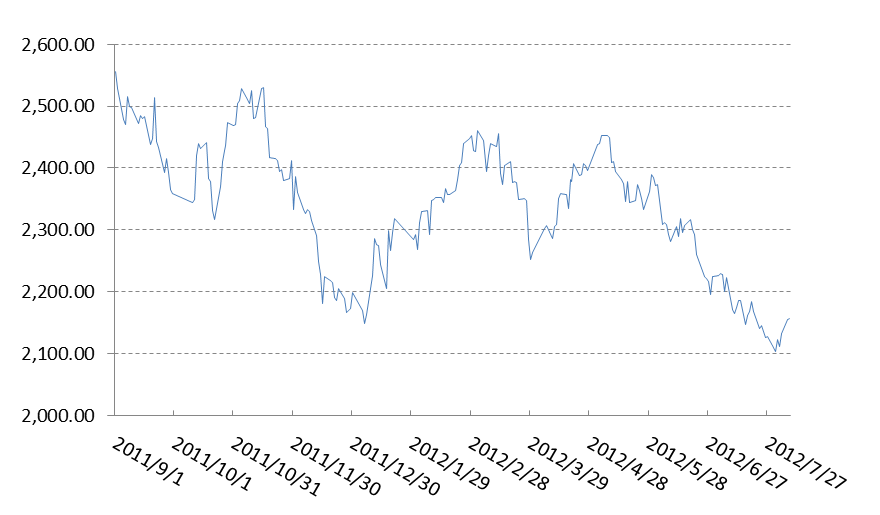
    图8-2上证指数收盘价时序图

      由此图，我们看到收盘价数据在这225交易日的时间内，有一定的趋势，常数项，以及周期性。我们应该将此序列判为非平稳时间序列.差分后，我们看到的数据在0周围频繁波动，这样的数据，我们可认为平稳。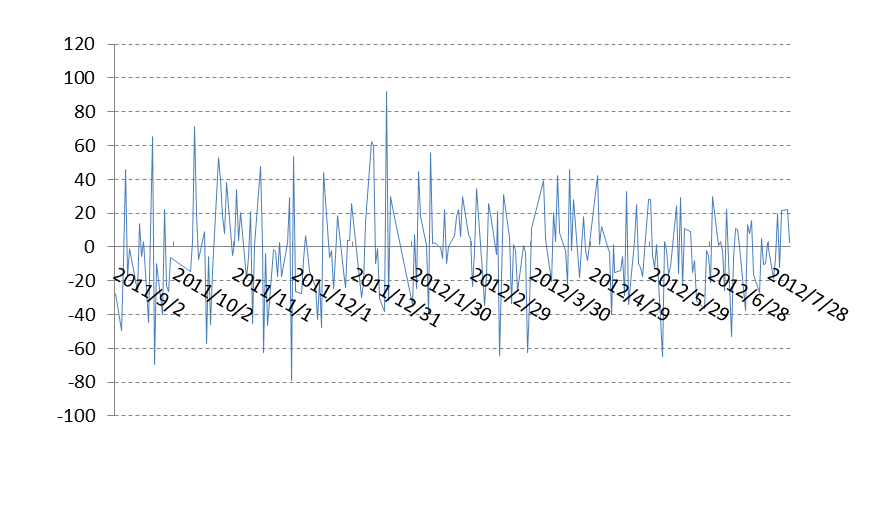

    图8-3上证指数收盘价差分时序图

    2)自相关函数（迅速衰减为0）
    自相关系数模型：Time_ACF
    范例：
      ret := Time_Acf(clos)[0:36];
      ret := Time_Acf(dclose)[0:36];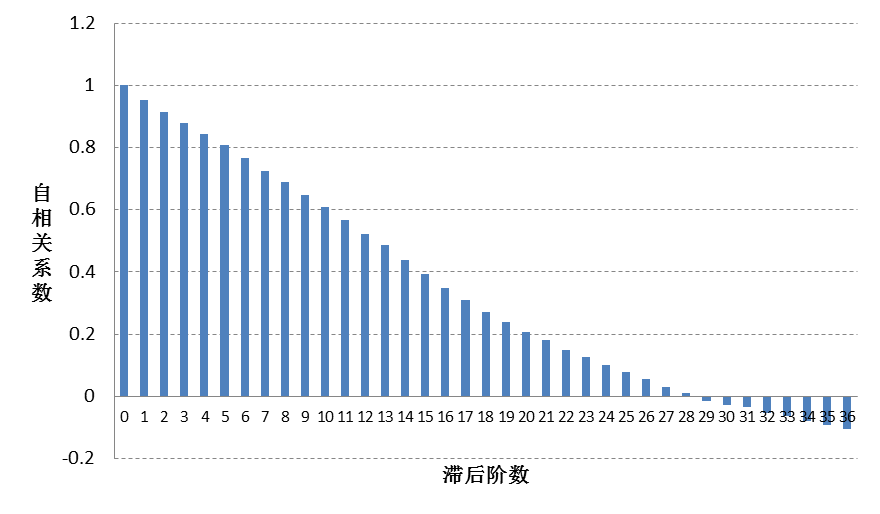


    图8-4上证指数收盘价自相关系数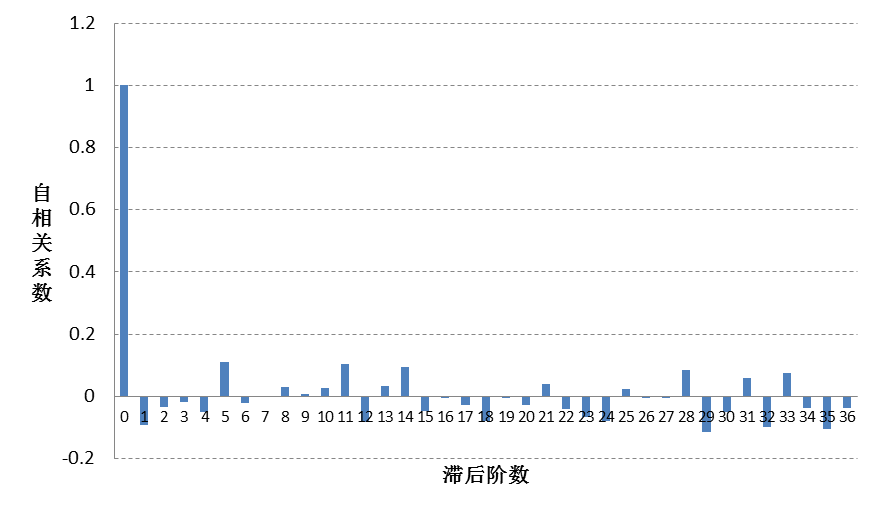


    图8-5上证指数收盘价差分后自相关系数

      自相关系数慢慢衰减为0，应该认为序列式非平稳时间序列.差分后的收盘价，自相关系数迅速衰减为0，应该认为收盘价差分序列是平稳时间序列.
    3)Time_DanielTest：Daniel平稳性检验
    Daniel平稳性检验模型：Time_DanielTest
    范例：
      ret := Time_DanielTest(clos,0.05);

    结果：array("Q-Value":-0.567,"T-Stat":-10.267,"P-Value":0.00,"Hypothesis":0)
    拒绝原假设，认为收盘价是非平稳时间序列.
      ret := Time_DanielTest(dclose,0.05);

    结果：array("Q-Value":0.034,"T-Stat":0.503,"P-Value":0.616,"Hypothesis":1)
    接受原假设，认为收盘价的差分是平稳时间序列.
    4)Times_ADFTest：单位根检验
    单位根检验模型：Times_ADFTest
    这里我们按照随机趋势序列（Style=1）来进行ADF检验。
      ret := Times_ADFTest(clos,0,1,"AIC",0,0.05);

    结果array("ADF-Stat":-2.0834,"5% Level":-2.8743)；
    收盘价是非平稳时间序列。
      ret := Times_ADFTest(clos,1,1,"AIC",0,0.05);

    结果：array("ADF-Stat":-16.3631,"5% Level":-2.8743)
    收盘价的差分是平稳时间序列。