在传统计量经济学模型中，干扰项的方差被假设为常数。但是许多经济时间序列呈现出波动的集聚性，在这种情况下假设方差为常数是不恰当的。我们可以使用Time_ARCH函数来检验回归残差是否服从同方差。
  为了刻画这种异方差性，Engel(1982)提出了ARCH模型，即自回归条件异方差模型。该模型的一般形式如下：
  均值方程：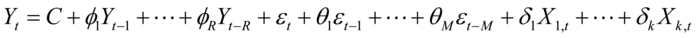

  方差方程：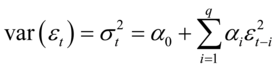
  均值方程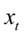是外生变量向量。方差方程表示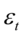的条件方差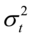由两部门构成，常数项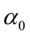和ARCH项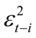。为保证条件异方差始终为正，要求方差方程中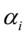非负，为保证自回归的稳定性，必须限制。
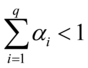  GARCH 模型：ARCH(p)模型解决了时间序列中的异方差问题，但在实际应用中常出现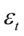的条件方差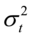依赖于很多期之前的变化量，因此必须估计很多个参数；另外，对大多数的q，无限定约束的估计常常会违背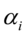非负的限定条件。为此，Bollerslev(1986)扩展了Engle的原始模型，提出了广义的自回归条件异方差GARCH模型，在方差方程中用一个或两个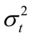的滞后项代替很多个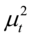的滞后值。一个高阶的ARCH模型可以由一个更为简洁、更易识别估算的低阶GARCH 模型来表达。GARCH(p,q)模型的方差方程的一般形式如下：

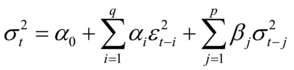
  方程右边的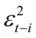是ARCH项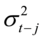，是GARCH项，q是ARCH项的阶数，p是GARCH项的阶数，为保证方差为正，要求方差方程所有系数为正。
  非对称的 ARCH 族模型：在金融时间序列的研究中经常会发现这种现象：不同信息的冲击常常表现为非对称的效应，即好消息和坏消息的冲击对波动性的影响程度不同。就许多股票而言，当前收益和未来波动之间有很强的负相关，收益增加时波动性减小，收益减小时波动性增加，这一趋势通常被称为杠杆效应。TARCH或GJR模型由Zakoian和Glosten，Jafanathan，Runkle(1994)提出，该模型中的方差方程如下：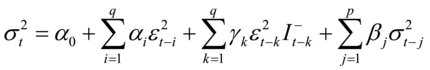

  其中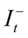是一个虚拟变量，当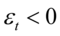时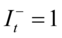，其余情况为0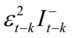，为非对称项，只要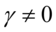，就存在非对称效应：好消息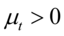会有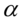倍的冲击，而坏消息会有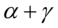倍的冲击。如果系数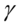显著不为0，我们就可以得到结论：数据包含非对称效应（门限效应）。如果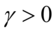，负冲击对波动性的影响大于正冲击，非对称效应的主要效果是使得波动加大，存在扛杆效应；如果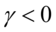，则非对称效应的主要效果是使得波动减小。
  指数GARCH模型或EGARCH模型是由Nelson(1991)提出的，采取条件方差对数的形式，方差方程形式如下：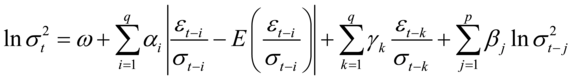

  等式左边是条件方差的对数，这意味着杠杆效应影响是指数而不是二次的，所以方差的预测一定是非负，在估计时对系数无需增加非负的限制，只要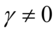，冲击的影响就存在着非对称性。只要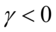，出现利好消息时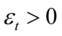，会带来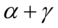的冲击。而出现利空消息时，会带来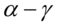的冲击。
GARCH-M模型：我们在GARCH模型的均值的末端加上一个条件异方差，就可以得到GARCH-M模型，该模型的方差方程和GARCH的方差方程是一样的。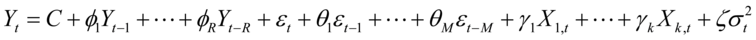

这样模型就可以衡量模型的波动对被解释变量的影响了。

广义自回归条件异方差模型：GarchFit
时间序列异方差的ARCH检验模型：Time_ARCHTest