天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 时间序列分析

GarchFit    

简述
广义自回归条件异方差模型，采用极大似然估计方法估计模型的参数
定义
GarchFit(ModelSpec:Array;y:array;x:Array;e0:Array;s0:Array;y0:Array);
参数
名称类型说明
ModelSpecArray模型设置项，为数据表类型，参考:表8-5
表8-5输入参数ModelSpec字段
字段 含义 类型 缺省值
VarianceModel 模型类别(Garch,GARCH-M,GJR,EGARCH) Varchar GARCH
Distribution 数据分布类型(Gaussian或者T) Varchar Gaussian
R AR项个数 Int 0
M MA项个数 Int 0
P GARCH项个数 Int 1
Q ARCH项个数 Int 1
DoF 自由度(T分布时有效) Int 程序计算
C 均值方程常数项初始值(NaN表示不含常数) Real 0
AR AR项初始值 Array array()
MA MA项初始值 Array array()
InMean 均值方程是否含条件方差方程 Bool FALSE
Regress 回归项初始值 Array array()
K 条件方差方程常数项初始值 Real 程序计算
GARCH GARCH项初始值 Array array()
ARCH ARCH项初始值 Array array()
Leverage Leverage项项初始值 Array array()
MaxFunEvals 调用目标次数 Int 100*变量个数
MaxIter 最大迭代次数 Int 400
TolFun 目标精度 Real 1.00E-06
TolCon 约束条件精度 Real 1.00E-06
TolX 变量精度 Real 1.00E-06
yarray原始数据，一维数字数组
xArray均值方程回归外生变量，二维数字数组，可缺省
e0Array自回归方程残差序列起始的几项取值，一维数字数组，可缺省
s0Array条件方程方差序列起始的几项取值，一维数字数组，可缺省
y0Array原始序列起始的几项取值，一维数字数组，可缺省
返回数组，各下标对应如下：
Ret["C"]：均值方程常数项
Ret["AR"]：均值方程AR项
Ret["MA"]：均值方程MA项
Ret["Regress"]：均值方程外生变量回归项
Ret["InMean"]：均值方程条件方差项，当选择模型为“GARCH-M”时存在
Ret["K"]：条件方差方程常数项
Ret["GARCH"]：条件方差方程GARCH项
Ret["ARCH"]：条件方差方程ARCH项
Ret["Leverage"]：条件方差方程杠杆项，当选择模型为“GJR”或者“EGARCH”时存在
Ret["LLF"]：残差的极大似然函数值
Ret["e"]：残差序列
Ret["h"]：条件方差序列
  • 范例


    以1995年1月至2000年8月日元兑换美元汇率值序列（JPY，如图8-9）为例介绍怎样用天软来进行ARCH建模（序列共1427个值）。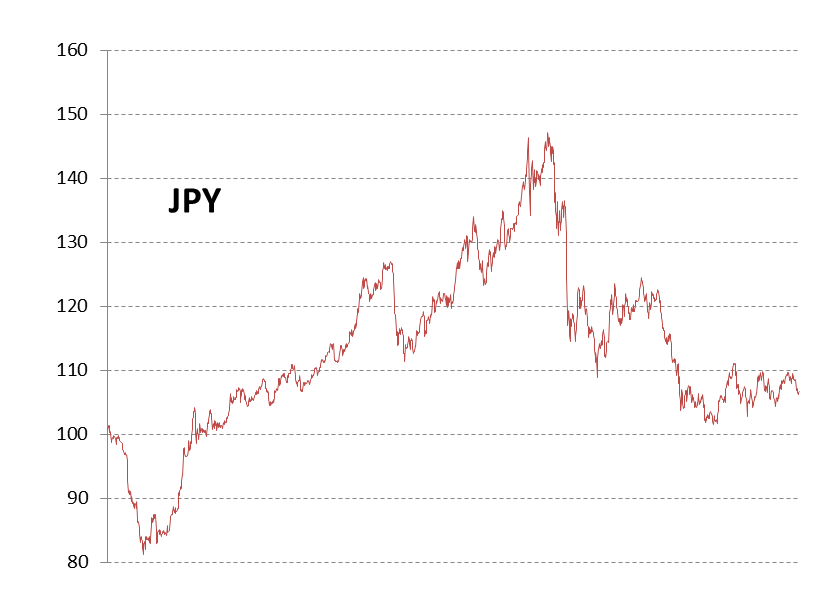

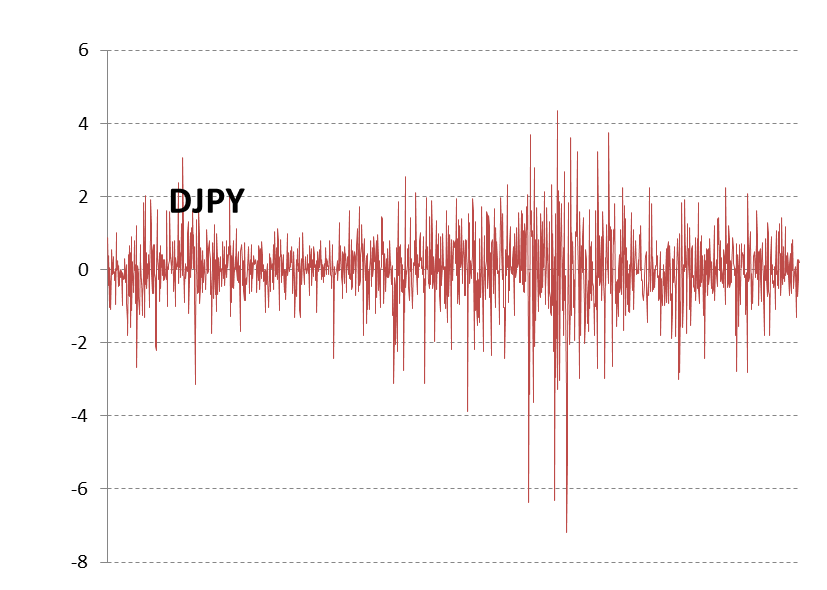
    图8-9日元兑换美元汇率值(JPY)序列图8-10DJPY时间序列
    JPY序列显然是一个非平稳时间序列，对JPY进行差分，DJPY表示收益，见图8-10，因为DJPY是一个平稳时间序列，应该使用DJPY建立时间序列模型。按照ARMA模型中讲的那样对DJPY拟合ARMA模型，根据自相关系数以及偏自相关系数，AIC准则等，我们最终将模型定为AR(3)模型。
    dJPY := diff(JPY);
    m := mean(dJPY);
    dJPY := dJPY-m;
    ret := ARMA(dJPY,3,0);
    得到的结果是：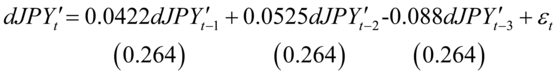



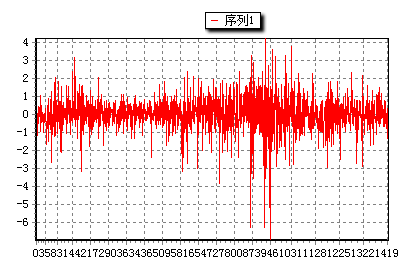
    图8-11 AR(3)残差
    该模型的残差如图8-11所示，我们怀疑残差含有异方差，使用Time_ARCHTest函数检验。
    Time_ARCHTest(ret["e"],1,0.05);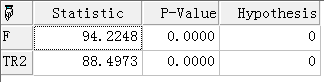

    图8-12 AR(3)残差
    拒绝原假设，认为模型含有异方差，建立ARCH模型，首先建立ARCH(7)模型(尝试多次，最大滞后选为7为宜)。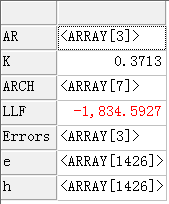

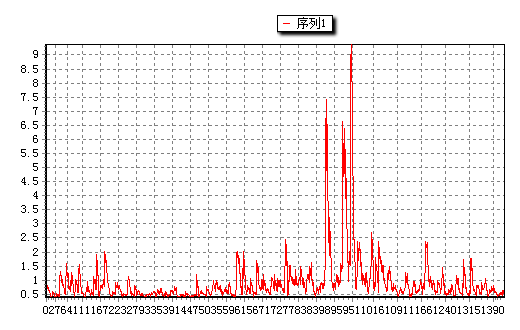
    图8-13ARCH模型结果图8-14异方差估计情况
    modelspec:= array(
        ("R":3,
        "M":0,
        "AR":NIL,
        "MA":NIL,
        "Regress":NIL,
        "VarianceModel":"GARCH",
        "C":nan,
        "P":0,
        "Q":7,
        "GARCH":array(),
        "ARCH":array(),
        "Leverage":NIL));
    t := garchfit(ModelSpec,dJPY);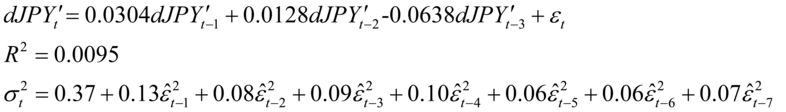

    得到的异方差如图8-14。ARCH模型中的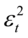的滞后项太多，应该尝试建立GARCH(1,1)模型：
    modelspec := array(
        ("R":3,
        "M":0,
        "AR":NIL,
        "MA":NIL,
        "Regress":NIL,
        "VarianceModel":"GARCH",
        "C":nan,
        "P":1,
        "Q":1,
        "GARCH":array(),
        "ARCH":array(),
        "Leverage":NIL));
    t := garchfit(ModelSpec,dJPY);


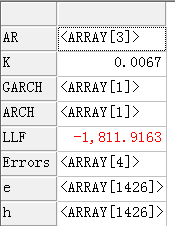
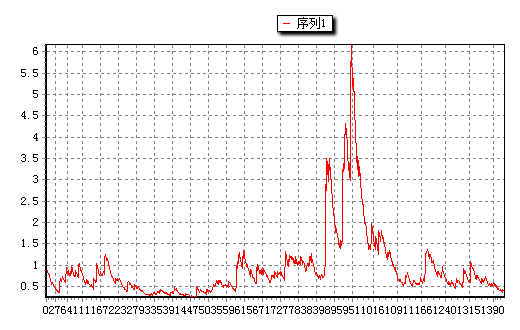
    图8-15GARCH模型结果图8-16方差估计情况
相关