天软金融分析.NET函数大全 > 金融报表分析 > 数学方法案例 > 投资组合

Portopt    

简述
计算带约束投资组合的有效前沿。
函数Protopt通过给定资产组合的预期收益率和协方差矩阵，计算投资组合有效边界，即相同的风险水平（标准差）下最大收益率的组合，或相同的预期收益率下，选择风险最小的组合。函数的输出分为两个部分，分别是“组合收益风险”：每个有效组合对应的预期收益率和标准差，以及“组合各资产权重”：每个有效组合对应的各个资产配置比例。
定义
portopt(Expreturn:array; ExpCov:array; Numports:int; Portreturn:array;     Conset:array):array
参数
名称类型说明
Expreturnarray一维实数数组，资产预期收益；
ExpCovarray二位实数数组，资产协方差矩阵；
Numportsint整数，求有效前沿组合数，可选，默认为10；
Portreturnarray一维实数数组，要求投资组合的回报率，可选，非空时 Numports失效；
Consetarray 数据表结构，资产约束信息，可选，默认为x>=0,sum(x)=1。
约束条件为:
1).A:*X <= B
2).Aeq:*x = Beq
3).Lb <= x <= Ub
其中，X为组合各个资产的权重，用户需给变量A、B、Aeq、Beq、LB、Ub的值。输出入格式例如:
Conset1:=array();
Conset1['A',0] := array((1,0,1));
Conset1['B',0] := array(0.5);
Conset1['Aeq',0] := array((1,1,1));
Conset1['Beq',0] := array(1);
Conset['Lb',0] := array(0.2,0,0);
返回array数组

1、投资组合的风险、投资组合的回报率； PortRisk | PortReturn

2、投资组合中各资产的权重。
  • 范例

    范例01：
    资产组合为三个申万一级行业指数：农林牧渔、采掘、化工
    是用历史数据计算每个资产的预期收益率和协方差矩阵
    将预期收益率和协方差矩阵输入 Portopt 函数计算有效前沿和对应的资产权重

    SetSysParam(pn_cycle(),cy_day());
    r:=pf_GetPortfolioRate(array('SW801010','SW801020','SW801030'),20190101T,20191231T,0);
     r:=r[:][1:];
    //对预期收益率和协方差矩阵年化
     expreturn:=mean(r);
     expcov:=Covariance(r);
     //计算包括最小风险组合和最大收益率组合在内的10个有效组合
     r:=Portopt(expreturn,expcov,10);
     return r;


    返回结果：

    对输出结果“组合收益风险”中的每个预期收益率和标准差画在坐标系上，横坐标为标准差，纵坐标为预期收益率，即得到“有效边界”。如下图: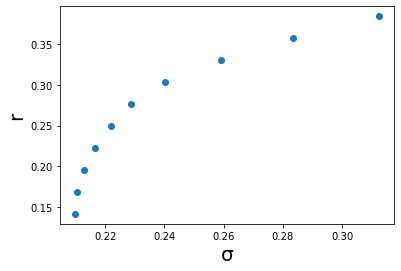

    范例02：参数Portreturn的用法：返回对应收益率下最小方差的资产组合
     SetSysParam(pn_cycle(),cy_day());
    r:=pf_GetPortfolioRate(array('SW801010','SW801020','SW801030'),20190101T, 20191231T,0);
     r:=r[:][1:];
     expreturn:=mean(r);
     expcov:=Covariance(r);
     //返回收益率为10%和15%且方差尽可能小的资产组合
     r:=Portopt(expreturn,expcov,10,array(0.1,0.15));
     return r;

    范例03：
    参数Conset的用法：设置资产组合的等式约束和非等式约束，设置方式为矩阵计算；设置单个资产权重的比例上界和下界；
    不等式约束：资产1、2的权重总和小于等于0.9实现过程：假设3个资产权重为X=((x1),(x2),(x3)),使矩阵与之相乘A:*X得到(1*x1+1*x2+0*x3)=x1+x2,在函数Portopt中控制约束条件：x1+x2<=B即x1+x2<=0.9，从而实现约束：资产1、2的总权重小于等于0.9
      即：A:=array((1,1,0));B:=array(0.9);
    等式约束：资产的权重总和等于1
    实现过程：假设3个资产权重为X=((x1),(x2),(x3)),使矩阵与之相乘Aeq:*X得到(1*x1+1*x2+1*x3)=x1+x2+x3,在函数Portopt中控制约束条件：x1+x2+x3=Beq即x1+x2+x3=1，从而实现约束：资产2和资产3的权重x1、x2、x3总和等于1

    即：Aeq:=array((1,1,1)); Beq:=array(1);
    r:=pf_GetPortfolioRate(array('SW801010','SW801020','SW801030'),20190101T,20191231T,0);
    r:=r[:][1:];
    expreturn:=mean(r);
    expcov:=Covariance(r);
    A:=array((1,1,0));
    B:=array(0.9);
    Aeq:=array((1,1,1));
    Beq:=array(1);
    //各个资产权重下界
    Lb:=array(0.2,0,0);
    //各个资产权重上界
    Ub:=array(0.8,0.8,0.8);
    Conset:=array();
    Conset['A',0]:=A;
    Conset['B',0]:=B;
    Conset['Aeq',0]:=Aeq;
    Conset['Beq',0]:=Beq;
    Conset['Lb',0]:=Lb
    Conset['Ub',0]:=Ub;
    r:=Portopt(expreturn,expcov,10,array(),Conset);
    return r;
相关