天软金融分析.NET函数大全 > 金融函数 > 组合评价 > 绩效归因 > 多期收益分解
在收益率分解过程中会遇到多期收益率无法跨期相加的问题,现
提供算术分解法解决多期收益率的分解。
假设R(p,t)为组合收益率,R(b,t)为基准收益率,r(1,t)、r(2,t)、r(3,t)分别为分解项
在单期下存在:
R(p,t)-R(b,t)=r(1,t)+r(2,t)+r(3,t)
经过调整后,单期存在:
ln(1+R(p,t))-ln(1+R(b,t))=k1*(r(1,t)+r(2,t)+r(3,t))
其中:
k1=(ln(1+R(p,t))-ln(1+R(b,t)))/(R(p,t)-R(b,t))
多期累加:
ln(1+Rp)-ln(1+Rb)=∑k1*(r(1,t)+r(2,t)+r(3,t))
经调整:
Rp-Rb=k2*∑k1*(r(1,t)+r(2,t)+r(3,t))
其中:
k2=(Rp-Rb)/((ln(1+Rp)-ln(1+Rb))
Pf_md_arithmetic
简述
多期收益率分解--算术几何法
在收益率分解过程中会遇到多期收益率无法跨期相加的问题,现
提供算术分解法解决多期收益率的分解。
假设R(p,t)为组合收益率,R(b,t)为基准收益率,r(1,t)、r(2,t)、r(3,t)分别为分解项
在单期下存在:
R(p,t)-R(b,t)=r(1,t)+r(2,t)+r(3,t)
经过调整后,单期存在:
ln(1+R(p,t))-ln(1+R(b,t))=k1*(r(1,t)+r(2,t)+r(3,t))
其中:
k1=(ln(1+R(p,t))-ln(1+R(b,t)))/(R(p,t)-R(b,t))
多期累加:
ln(1+Rp)-ln(1+Rb)=∑k1*(r(1,t)+r(2,t)+r(3,t))
经调整:
Rp-Rb=k2*∑k1*(r(1,t)+r(2,t)+r(3,t))
其中:
k2=(Rp-Rb)/((ln(1+Rp)-ln(1+Rb))
定义
Pf_md_arithmetic(T1:Array;T2_:Array of number;T3:Array;Ret:Array):TABLE
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| T1 | Array | Array,一维数组:组合收益率(%) |
| T2_ | Array of number | 一维数组:基准收益率(%) |
| T3 | Array | Array,一维或二位数组:收益分解项(%),要求每期 收益分解项+基准收益率=组合收益率,为一维数组时,等同于列名为0的二维数组。 |
| Ret | Array | Array,变参,返回经调整后的各分解项每期的收益 |
| 返回 | TABLE | 字段含义说明:
'组合(%)':区间组合累计收益率(%) '基准(%)':区间基准累计收益率(%) '超额(%)': 组合(%) - 基准(%) '分解项':合成后的多期分解项收益率(%) 有恒等关系: '组合(%)' - '基准(%)' = '超额(%)' = sum('分解项')" |
- 范例//组合:各资产等权,每期再平衡;以债券收益为基准
data := TSUT_Data_ZSZF();
data[:,1:] := data[:,1:]/4;
data[:,'组合(%)'] := sum(data[:,1:],1);
FJ:=select ["沪深300"],["中证500"],["中证1000"] from data end;
return pf_MD_Arithmetic(data[:,"组合(%)"],data[:,"国债指数"],FJ);
返回结果: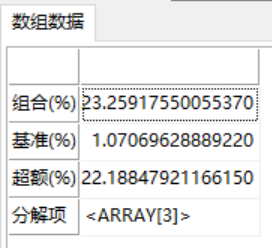
相关