天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 优化

Prog_Q    

简述
二次规划问题求解(采用作用集方法)
Prog_Q(H,f,A,b)
求解不等式约束
Prog_Q(H,f,A,b,Aeq,beq)
求解不等式约束、等式约束
Prog_Q(H,f,A,b,Aeq,beq,LB,UB)
求解不等式约束、等式约束、上下界限约束
Prog_Q(H,f,A,b,Aeq,beq,LB,UB,x0,options)
模型表达：
min= `x* H* x /2 + sum(f*x)
st. A:*x<=b

Aeq :* x = Beq;
lb<x<ub;
定义
Prog_Q (H:array;f:array;A:array;B:array;Aeq:array;Beq:array;Lb:array;Ub:array;x0:array;options):array;
参数
名称类型说明
HArray,TableArray 二次型，正定二次型二维数字数组，不可缺省
fArray,TableArray线性目标，一维数字数组，不可缺省
aArray,TableArray线性约束，二维数字数组，不可缺省
bArray,TableArray线性约束，一维数字数组，不可缺省
AeqArray,TableArray 线性约束，二维数字数组，缺省为空
BeqArray,TableArray 线性约束，一维数字数组，缺省为空
LbArray,TableArray 下界约束，一维数字数组，缺省为空
UbArray,TableArray 上界约束，一维数字数组，缺省为空
x0Array,TableArray 初始值，一维数组
optionsArray,TableArray 选项设置,数据表类型，缺省为array('maxiter':  400 ,  //最大迭代次数'tolcon':  1.0e-6, //约束容忍误差'tolfun' :  1.0e-6 , //目标最小误差'tolx' :   1.0e-6  //变量最小变化)
返回Array,TableArray返回结果:数据表类型ret["X"] : 变量取值，一维数字数组ret["Fval"] :规划目标值，实数ret["Error_M"] : 结果信息，整数，具体含义参考[Prog_L]中的返回信息ret["Iter"] : 迭代次数，整数
  • 范例

    H:= array((2,0),(0,2));    //二次项
    f := array(-8,-10);      //一次项
    A := array((3,2));b := array(6); //不等式约束
    Aeq := array((1,1));beq := array(2.54);  //等式约束
    Lb := array(0,0);
    Ub := array();   //上下界约束
    ret := prog_q(h,f,a,b,aeq,beq,lb,ub);

    结果：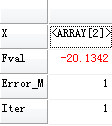
    参考
    Prog_L Prog_N Prog_M NonLP_Fminsearch NonLP_Fminbnd 
相关