主成分法是通过线性变换，将原来的多个指标组合成相互独立的少数几个能充分反映总体信息的指标，从而在不丢掉重要信息的前提下避开变量间共线性问题，便于进一步分析。在主成分分析中提取出的每个主成分都是原来多个指标的线性组合。比如有两个原始变量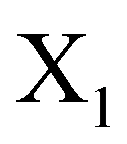和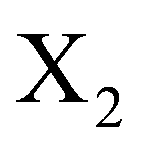，则一共可提取出两个主成分：
(7.22)
原则上如果有n个变量，则最多可以提取出n个主成分，但如果将它们全部提取出来就失去了该方法简化数据的意义。一般情况下提取出2-3个主成分（已包含了85%以上的信息），其他的可以忽略不计。
主成分分析的基本原理是将解释变量转换成若干个主成分，这些主成分从不同侧面反映解释变量的综合影响，并且互不相关。因此，可以将被解释变量关于这些主成分进行回归，再根据主成分与解释变量之间的对应关系，求得原回归模型的估计方程。
主成分回归的具体步骤：
1)对原始样本数据做标准化处理，得到解释变量的相关系数矩阵R。
2)计算R的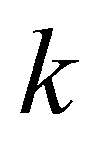个特征值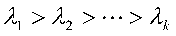，以及相应的标准化特征向量。
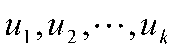3)利用特征值检验多重共线性。模型存在多重共线性时，至少有一个特征值近似地等于零，不妨设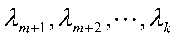近似为零，这表明解释变量之间存在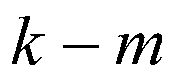个线性相关关系。
4)设多元线性模型为，标准化后的解释变量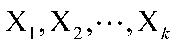的k个主成分为
 (7.23)
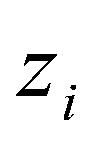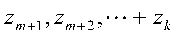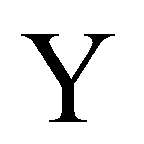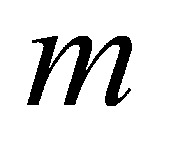其中互不相关，并且近似为零。将标准化的被解释变量关于个主成分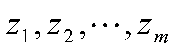进行回归，得
(7.24)
5)根据主成分与解释变量之间的关系式（7-23），将其代入主成分回归方程式（7-24），求得用标准化数据表示的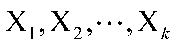回归方程：
(7.25)
6)系数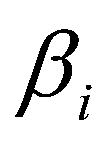与原模型中参数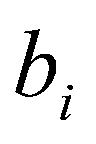之间的关系为
(7.26)
(7.27)
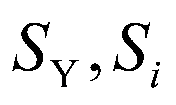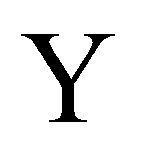其中，分别为和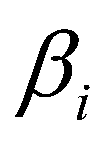的标准差，由此可以计算出原回归模型中的参数，进而得到:
(7.28)

主成分回归模型：Regress_pri