天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 数值计算 > 矩阵运算及分解
mt_decompose_svd
简述
矩阵的奇异值(SVD)分解定义
mt_decompose_svd(A; U; S; D:Array Of Real);mt_decompose_svd(A; S);mt_decompose_svd(A;U;S);
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| A | Array Of Real) | 待分解的m*n矩阵 |
| S | Array Of Real) | 变参返回A的奇异值,一维数组 |
| U | Array Of Real) | 变参返回A的左奇异矩阵,二维数组 |
| D | Array Of Real) | 变参返回A的右奇异矩阵,二维数组 |
- 算法
假设矩阵A为一个m×n的矩阵,定义矩阵A的SVD分解为:
A=USDT
其中U为m×m矩阵,S为m×n矩阵,D为个n×n矩阵,其中U、D都为酉矩阵。
求解U、S、D三个矩阵的步骤如下:
1)根据下式求解方阵ATA的特征值与特征向量:
ATAdi=λidi
n个特征向量di组成右奇异矩阵D。
同理,利用AATui=λiui计算可得左奇异矩阵U。
2)求奇异值矩阵S(除了对角线为奇异值σi,其余位置为0)可根据以下公式求得:
AD=USAdi=uiσi
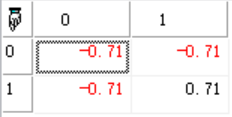
(也可通过σi=λi计算),即可计算出奇异值矩阵S。范例//计算矩阵A的SVD分解
A:=array((0,1),(1,1),(1,0));
Mt_Decompose_SVD(A,U,S,D);
//反推初始矩阵A,使用U:*(eye(3,2)*S):*`D;
return array((U),(S),(D));
//结果:
U,S,D矩阵分别为: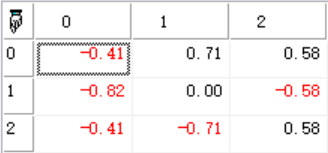

相关