ARMA模型拟合

ARMA模型有两个预先要给定的参数，p，q。这两个参数用户可以通过观察自相关系数以及偏自相关系数初步给定，再使用信息准则最小原则在旁边寻找。

偏自相关系数模型：Time_PACF

表8-3 ARMA模型定阶原则

模型定阶	自相关系数	偏自相关系数
AR(p)模型	拖尾，指数衰减缓慢	P阶截尾
MA(q)模型	q阶截尾	拖尾，指数衰减缓慢
ARMA(p,q)模型	拖尾，指数衰减缓慢	拖尾，指数衰减缓慢

ret := array(); for i := 1 to 12 do
begin
temp := Time_RandomTest(dpop,i,0.05);
ret[i-1] := array("Qm-Stat":temp["Qm-Stat"],"P-Value":temp["P-Value"]);
end
ret := `array("lag":1->12,"ACF":Time_ACF(dpop)[1:12],"PACF":Time_ACF(dpop)[1:12])|ret;

表 8-4 人口差分数据的(偏)自相关系数,QM检验量

lag	ACF	PACF	Qm-Stat	P-Value
1	0.6137	0.6137	20.738	0.0000
2	0.2572	0.2572	24.452	0.0000
3	0.1391	0.1391	25.561	0.0000
4	0.0807	0.0807	25.942	0.0000
5	0.0057	0.0057	25.944	0.0001
6	-0.054	-0.054	26.12	0.0002
7	-0.132	-0.132	27.206	0.0003
8	-0.146	-0.146	28.567	0.0004
9	-0.178	-0.178	30.626	0.0003
10	-0.216	-0.216	33.738	0.0002
11	-0.227	-0.227	37.256	0.0001
12	-0.214	-0.214	40.482	0.0001

我们可以初步将模型定为ARMA(1,0)。使用AIC准则，可以知道模型在ARMA(1,0)时，AIC统计量最小，所以我们给数据DLGDP拟合ARMA(1,0)模型。
自回归移动平均模型:ARMA
范例:

m := mean(dpop);
dpop_ := dpop-m;
return ARMA(dpop_,1,0);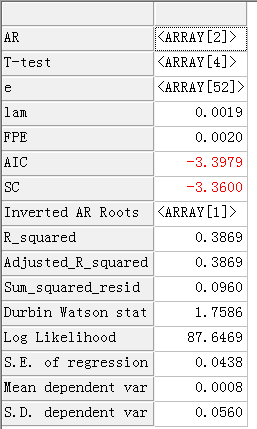

图8-8：人口数据差分拟合AR(1)模型
ARMA得到的最后估计式是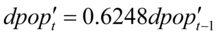

。

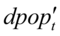表示中心化的

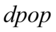序列。

ARMA模型拟合 复制链接

ARMA模型拟合