TSL语言基础 > 数学与统计教程 > 时间序列分析 > ARMA模型
随机性检验
随机性检验模型:Time_RandomTest
我们来查看下,上证收盘价差分后的数据的随机性检验:ret := array();
for i := 1 to 36 do
begin
temp := Time_RandomTest(dclose,i,0.05);
ret[i-1] := array(temp["Qm-Stat"],temp["P-Value"]);
end
return ret;
表 8-1 上证收盘价差分后数据随机性检验滞后阶数 QM统计量 P值 滞后阶数 QM统计量 P值 1 1.99 0.158 19 15.081 0.717 2 2.286 0.319 20 15.271 0.761 3 2.377 0.498 21 15.624 0.79 4 2.991 0.559 22 16.017 0.815 5 5.771 0.329 23 17.192 0.8 6 5.894 0.435 24 18.866 0.759 7 5.895 0.552 25 19.013 0.797 8 6.1 0.636 26 19.021 0.836 9 6.108 0.729 27 19.029 0.869 10 6.266 0.792 28 20.937 0.828 11 8.771 0.643 29 24.41 0.708 12 10.422 0.579 30 25.039 0.723 13 10.691 0.637 31 25.979 0.722 14 12.854 0.538 32 28.552 0.642 15 13.37 0.574 33 30.08 0.613 16 13.373 0.645 34 30.451 0.642 17 13.585 0.696 35 33.369 0.547 18 15.074 0.657 36 33.769 0.575
由以上结果,我们看到QM检验的结果基本上都认为差分序列为纯随机序列,没有分析的价值.
以下我们再来看个例子:1949年到2001年的中国人口时间序列数据,如表8-2.
表 8-2 中国人口时间序列数据(单位:亿人)年份 人口 年份 人口 年份 人口 年份 人口 年份 人口 1949 5.4167 1960 6.6207 1971 8.5229 1982 10.159 1993 11.8517 1950 5.5196 1961 6.5859 1972 8.7177 1983 10.2764 1994 11.985 1951 5.63 1962 6.7295 1973 8.9211 1984 10.3876 1995 12.1121 1952 5.7482 1963 6.9172 1974 9.0859 1985 10.5851 1996 12.2389 1953 5.8796 1964 7.0499 1975 9.242 1986 10.7507 1997 12.3626 1954 6.0266 1965 7.2538 1976 9.3717 1987 10.93 1998 12.4761 1955 6.1465 1966 7.4542 1977 9.4974 1988 11.1026 1999 12.5786 1956 6.2828 1967 7.6368 1978 9.6259 1989 11.2704 2000 12.6743 1957 6.4653 1968 7.8534 1979 9.7542 1990 11.4333 2001 12.7627 1958 6.5994 1969 8.0671 1980 9.8705 1991 11.5823 1959 6.7207 1970 8.2992 1981 10.0072 1992 11.7171 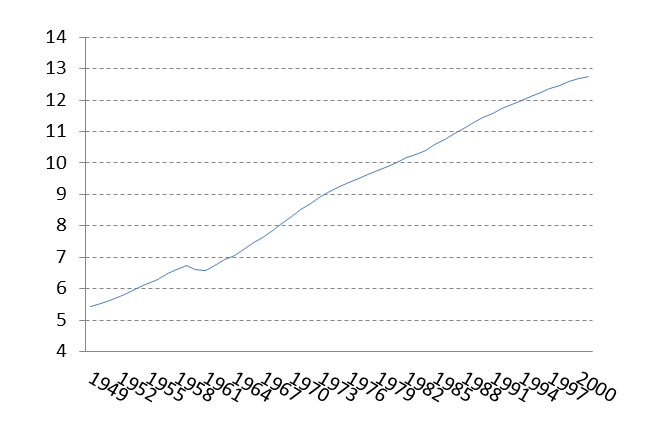
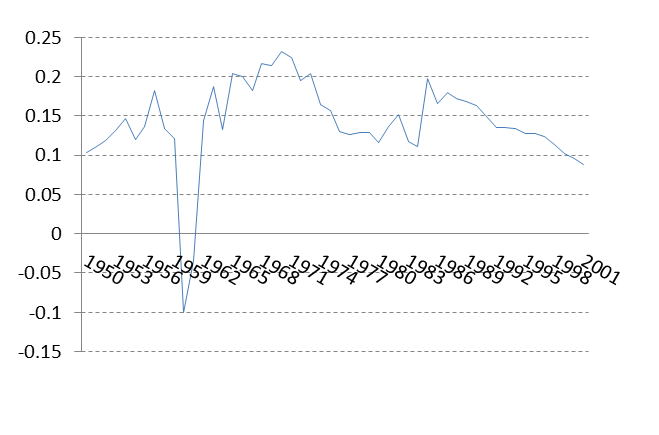
图8-6:人口数据图8-7:人口数据差分pop := array(5.41669999999999,5.51959999999999,5.63,5.7482,5.8796,6.0266,
6.1465,6.2828,6.4653,6.5994,6.7207,6.6207,6.5859,6.7295,6.9172,7.0499,7.2538,
7.4542,7.6368,7.8534,8.0671,8.2992,8.5229,8.7177,8.92109999999999,9.0859,9.242,
9.3717,9.4974,9.6259,9.7542,9.8705,10.0072,10.159,10.2764,10.3876,10.5851,
10.7507,10.93,11.1026,11.2704,11.4333,11.5823,11.7171,11.8517,11.985,12.1121,
12.2389,12.3626,12.4761,12.5786,12.6743,12.7627);
ret := Times_ADFTest(pop,0,1,"AIC",0,0.1); //检验平稳性,结果显示,不平稳
dpop := time_diff(pop);
ret := Times_ADFTest(dpop,0,1,"AIC",0,0.1); //检验平稳性,结果显示序列平稳
经检验我们可以做到pop是非平稳时间序列,而dpop是平稳时间序列,知道了这个,
相关