TSL语言基础 > 数学与统计教程 > 优化方法
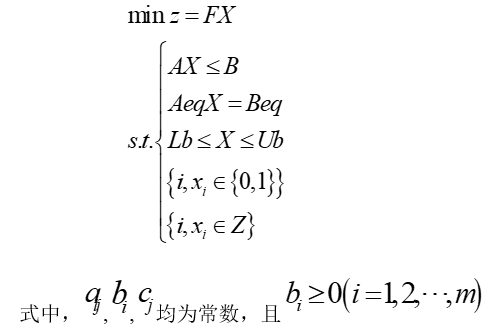
Prog_L：使用单纯形法，和起作用集法，系统默认使用起作用集方法求解线性规划问题，即求解目标都为线性和约束条件都为线性的规划问题
线性规划
简述
线性规划是数学规划的一个重要分支，也是最简单、最基础的一类问题，它历史悠久，理论较成熟，方法也校完善。这里我们的模型把整数规划也包含进来。
Prog_L：使用单纯形法，和起作用集法，系统默认使用起作用集方法求解线性规划问题，即求解目标都为线性和约束条件都为线性的规划问题
定义
Prog_L (f:array;A:array;B:array;Aeq:array;Beq:array;Lb:array;Ub:array;x0:array;options:array;ozarr:array;intarr:array):array;
参数
| 名称 | 类型 | 说明 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | array | 线性目标，一维数字数组，不可缺省 | ||||||||||||||||||
| a | array | 线性约束，二维数字数组，不可缺省 | ||||||||||||||||||
| b | array | 线性约束，一维数字数组，不可缺省 | ||||||||||||||||||
| Aeq | array | 线性等式约束，二维数字数组，缺省为空 | ||||||||||||||||||
| Beq | array | 线性等式约束，一维数字数组，缺省为空 | ||||||||||||||||||
| Lb | array | 下界约束，一维数字数组，缺省为空 | ||||||||||||||||||
| Ub | array | 上界约束，一维数字数组，缺省为空 | ||||||||||||||||||
| x0 | array | 初始值，一维数组 | ||||||||||||||||||
| options | array | 方法设置选项，数据表类型，见表9-1 | ||||||||||||||||||
| Ozarr | array | 01约束条件，第1个变量为01变量则ozarr := array(0) | ||||||||||||||||||
| Intarr | array | 整数约束条件，第2,3两个变量为整数变量则 intarr:=array(1,2)
表9-1 线性规划方法选项options字段
| ||||||||||||||||||
| 返回 | array | 数组。 |
- 范例
例：某车间有一批长度为7.4m的同型钢管，砍用它们来做100套钢架，已知每套钢架需用长2.9m、2.1m和1.5m的钢管各一根。问如何下料方可使所用材料最省
解：因为所需钢材总长度是固定的，所以要使用料的根数最少，也就是要使裁下来的残料最少、而残料的多少取决于裁取方法，故设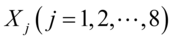
为按第j种方法裁取钢管的跟数，则对各种可能的裁取方法所产生的残料：
所裁长度/m 裁料方案 所需根数 1 2 3 4 5 6 7 8 2.9 2 1 1 1 0 0 0 0 100 2.1 0 0 2 1 2 1 3 0 100 1.5 1 3 0 1 2 3 0 4 100 残料长度/m 0.1 0 0.3 0.9 0.2 0.8 1.1 1.4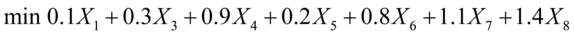 
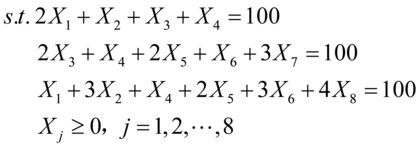
f := array(0.1,0,0.3,0.9,0.2,0.8,1.1,1.4);
a := array();
b := array();
aeq := array((2,1,1,1,0,0,0,0),(0,0,2,1,2,1,3,0),(1,3,0,1,2,3,0,4));
beq := array(100,100,100);
lb := array(0,0,0,0,0,0,0,0);
ub := array();
x0 := array();
options := array();
Ozarr := array();
Intarr := array(0,1,2,3,4,5,6,7);
return prog_L(f,a,b,aeq,beq,lb,ub,x0,options,ozarr,Intarr);
结果：
array("X":
(10.00,30.00,50.00,0.00,0.00,0.00,0.00,0.00),"Fval":16.00,"Error_M":1,"Iter":8)
"Error_M"的各输出值的含义详见表9-2。
表9-2 结果信息"Error_M"含义Error_M取值 含义 1 函数得到收敛的解 3 目标函数值变化小于设定精度 4 发现局部最优值 5 方向倒数小于精度 0 达到迭代次数 -1 算法终止 -2 没有发现可行解 -3 发散问题 -4 无可行下降方向 -7 不能继续求解，问题可能病态
相关