事件或变量的独立性，既是许多统计推断方法的前提条件，又是统计推断的对象。独立性检验，指关于独立性假设“事件（或变量）相互独立”的检验；检验一般以用列联表表示的联合频数分布为基础。
  随机变量X,Y的分布函数分别是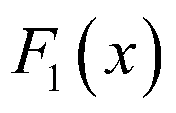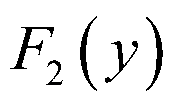，，且联合分布为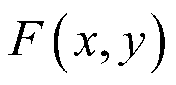，则X与Y的独立性问题归结为假设检验问题：
  
  首先，我们先介绍列表检验法:
  列表检验法是非常重要且简便易行的一种非参数检验，它既可以用于独立性，样本齐一性和随机性等假设的检验。
  若X,Y是分类变量，分别有r种取值，nij标示Xi与Yj同时出现的频数
  表7-2           r*s列联表

	Y1	Y2	…	Ys	总和
X1	n11	n12	…	n1s	n1.
…	…	…	…	…	…
Xr	nr1	nr2	…	nrs	nr.
总和	n.1	n.2	…	n.s	n

  这样独立性的原假设，我们可以写成

其中
，从而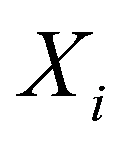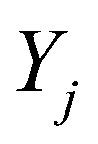，同时出现的频数应该是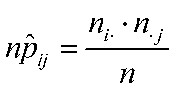，由此构建我们的统计量：
    (6.21)

独立性检验模型：Hypoth_IndepTest