本节中，我们将介绍几种判断一组数据是否服从给定分布的假设检验。正态分布是许多检验的基础，比如F检验，t检验，卡方检验等在总体不是正太分布是没有任何意义。因此，对一个样本是否来自正态总体的检验是至关重要的。当然，我们无法证明某个数据的确来自正态总体，但如果使用效率高的检验还无法否认总体是正太的检验，我们就没有理由否认那些和正太分布有关的检验有意义。
  NormPlot的基本思路是使用给定数据的经验分布与对应标准正态分布作比较，得到的散点图如果近似于一条直线，则我们认为该样本服从正态分布。

基于正态概率纸的正态性检验模型：NormPlot

范例:
返回结果：
array(
("采样位数":0.171976955840364,"理想位数":-1.64484977722168),
("采样位数":0.301570532377809,"理想位数":-1.03643536567688),
("采样位数":0.470976530341431,"理想位数":-0.674489885568619),
("采样位数":0.479131903499365,"理想位数":-0.38532167673111),
("采样位数":0.678062069928274,"理想位数":-0.125661492347717),
("采样位数":0.735156666953117,"理想位数":0.125661492347717),
("采样位数":0.739045920781791,"理想位数":0.38532167673111),
("采样位数":0.780685598030686,"理想位数":0.674489885568619),
("采样位数":0.817699506180361,"理想位数":1.03643536567688),
("采样位数":0.828364443266764,"理想位数":1.64484977722168))
QQ图形：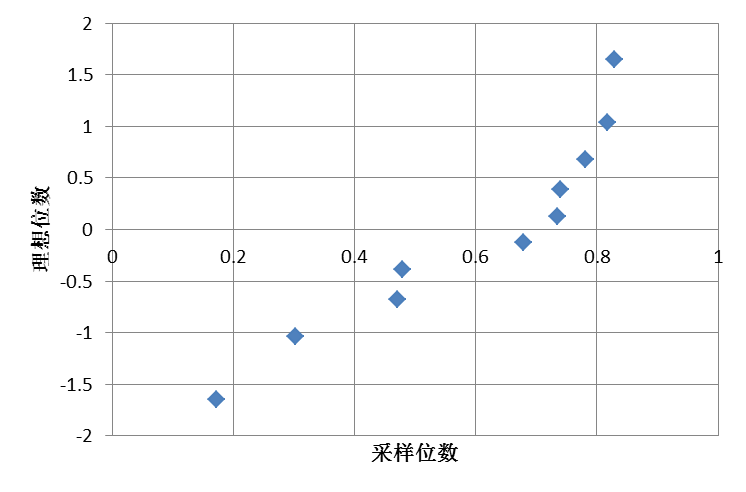
  
图6-1 QQ图
  返回结果：0.911334081735257

  从以上结果，我们可以有理由相信，该样本来自正态总体。这种方法，虽然比较直观，但是，我们不知道什么样的一个什么样的拟合程度才是我们需要的。
下面我们再来介绍下Kolmogorov-Smirnov检验的基本思路：
  原假设：随机样本数据服从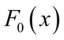分布
  
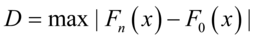
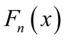表示一组随机样本的累计概率函数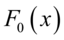，表示分布的分布函数。
当原假设为真时，D的值应较小，若过大，则怀疑原假设，从而，拒绝域为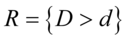

ks检验模型：Hypoth_Kstest

lillietest检验模型：Hypoth_lillietest