天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 时间序列分析
建议使用ARMA模型替换,移动平均模型,MA(q)模型,用条件最小二乘法去估计q阶移动平均模型的系数,返回结果有移动平均系数、残差方差、预测值及预测波动。
估计过程如下:
MA(q)模型:
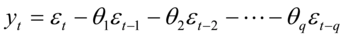
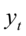 具有逆转形式:
具有逆转形式: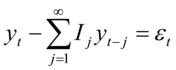
用算子形式比较,可得:
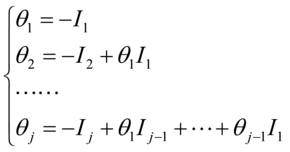 s
s
条件最小二乘法使得下列残差平方和最小:
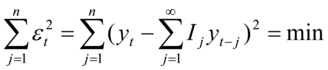
可将上述转化为矩阵形式,先求得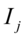 的取值,在利用上上式计算移动平均系数
的取值,在利用上上式计算移动平均系数
如有常数,则常数项为原序列的均值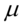 。
。
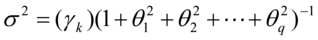 ,
,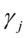 为自协方差
为自协方差
其中:yt为原序列零均值化的新序列,μ为原序列的均值,θq为移动平均系数,εt是零均值,方差为σ2的平稳白噪声
Time_MAq
简述
建议使用ARMA模型替换,移动平均模型,MA(q)模型,用条件最小二乘法去估计q阶移动平均模型的系数,返回结果有移动平均系数、残差方差、预测值及预测波动。
估计过程如下:
MA(q)模型:
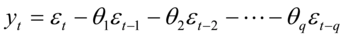
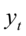 具有逆转形式:
具有逆转形式: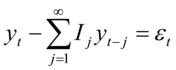
用算子形式比较,可得:
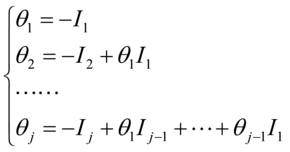 s
s
条件最小二乘法使得下列残差平方和最小:
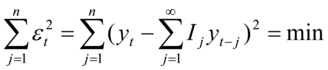
可将上述转化为矩阵形式,先求得
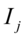 的取值,在利用上上式计算移动平均系数
的取值,在利用上上式计算移动平均系数
如有常数,则常数项为原序列的均值
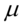 。
。
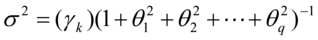 ,
,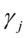 为自协方差
为自协方差
其中:yt为原序列零均值化的新序列,μ为原序列的均值,θq为移动平均系数,εt是零均值,方差为σ2的平稳白噪声
定义
Time_MAq(y:Array;Q:Integer;L:Integer):Array;
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| Y | Array | 样本序列,为一维数组类型; |
| q | Integer | 移动平均阶数; |
| l | Integer | 预测步长; |
相关