天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 时间序列分析
AR(p)模型:
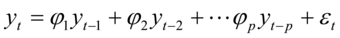
其中: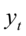 为原序列零均值化的新序列,
为原序列零均值化的新序列,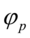 是自回归方程系数,
是自回归方程系数,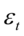 是零均值,方差为
是零均值,方差为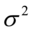 的平稳白噪声
的平稳白噪声
AR
简述
自回归模型,AR(p)模型,选择使用最小二乘,Yule-Walker方法,Foiward-backward,Geometric lattice,Burg’s lattice-bas去估计p阶自回归模型的系数,返回结果有自回归系数、残差方差、预测值及预测波动等信息
AR(p)模型:
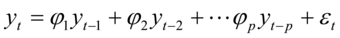
其中:
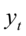 为原序列零均值化的新序列,
为原序列零均值化的新序列,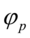 是自回归方程系数,
是自回归方程系数,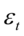 是零均值,方差为
是零均值,方差为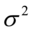 的平稳白噪声
的平稳白噪声定义
AR(Y:Array of Real;P:Integer; Approach:String):Array;
参数
| 名称 | 类型 | 说明 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y | Array of Real | 样本序列,为一维数组类型,注意要零均值化 | |||||||||||
| P | Integer | 自回归阶数 | |||||||||||
| Approach | String | 估计方法
返回结果: Ret["AR"]:参数估计结果, 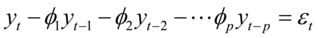 ,第一项为1 ,第一项为1
Ret["T-test"]:AR模型参数的T检验 Ret["e"]:残差信息 Ret["LossFunction"]:残差平方和/n-p Ret["FPE"]:预测最大误差 Ret["AIC"]:模型的AIC信息准则 Ret["SC"]:模型的SC信息准则 Ret["Inverted AR Roots"]:特征方程的特征根 Ret["R_squared"]:AR模型的可决系数 Ret["Adjusted_R_squared "]:AR模型的修正可决系数 Ret["Sum_squared_resid"]:AR模型的离差平方和 Ret["Durbin Watson stat"]:DW统计量 Ret["Log Likelihood"]:对数极大似然值 Ret["S.E. of regression"]:回归标准差 |
- 范例elps:=Randnorm(0,1,200);
y:=array();
y[0]:=0;
y[1]:=0;
for i:=2 to 199 do
y[i]:=-0.5*y[i-1]+0.3*y[i-2]+elps[i];
return AR(y,2,'ls');
结果: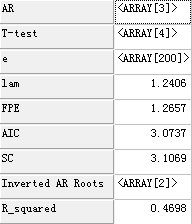
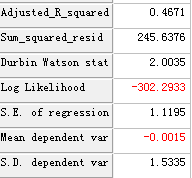 Time_ACF Time_PACF Time_RandomTest ARMA参考
Time_ACF Time_PACF Time_RandomTest ARMA参考
相关
FAQ/知识库链接