天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验
Regression_WLS
简述
加权最小二乘法回归, WType为0时,必须给出m1 权重系数下限,m2 权重系数上限,steps 步长,用于计算最优权重,WType为1时,必须给出wweight权重向量。定义
Regression_WLS(Y:array;X:array;alpha:real;constant:boolean;WType:boolean;m1:real;m2:real;steps:real;wweight:array):Array;
参数
| 名称 | 类型 | 说明 | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | array | 因变量,一维数字数组 | ||||||||||||||||||||||||||||
| x | array | 自变量,二维数字数组 | ||||||||||||||||||||||||||||
| alpha | real | 显著性水平,实数 | ||||||||||||||||||||||||||||
| constant | boolean | 是否有常数项,0没有常数项,1 有常数项 | ||||||||||||||||||||||||||||
| Wtype | boolean | 权重选择如下:
| ||||||||||||||||||||||||||||
| m1 | real | 权重系数下限,实数 | ||||||||||||||||||||||||||||
| m2 | real | 权重系数上限,实数 | ||||||||||||||||||||||||||||
| steps | real | 步长,实数 | ||||||||||||||||||||||||||||
| wweight | array | 权重向量,一维数字数组,当WType设置为1时,需要此参数的输入
返回结果:
|
- 算法
加权最小二乘法算法说明:
因变量y和自变量x长度都是n,假设满足最小二乘回归的经典假设时,y对x进行回归,形如:
yi=β0+β1x1+β2x2+…+βkxk+μi,i=1,2,3,...,n
用矩阵形式表示为:
Y=Xβ+μ
其中,ββ为系数矩阵,Y为因变量的n个观测值组成的n×1的列向量,X为一个n×(k+1)的矩阵。
一般的多元线性回归中,假设满足最小二乘回归的经典假设时,β系数的计算公式为:
β=(X'X)-1 X'Y
但是,当误差项μi存在异方差时,违反了经典假定中的同方差性的假定条件,加权离差平方和为:
Qw=i=1nwi(yi-β0-β1x1-β2x2-…-βkxk)^2
其中,wi为给定的第i个观测值的权数,加权最小二乘法就是寻找β0,β1,β2,…,βkβ0,β1,β2,…βk的估计值使Qw达到最小,记:
Wdiag=w1wn
加权最小二乘估计WLS的矩阵可表达为
βw=(X'WdiagX)-1X'WdiagY范例Y:=array(55.0,65.0,70.0,80.0,79.0,84.0,98.0,95.0,90.0,75.0,74.0,110.0,113.0,125.0,108.0,115.0,140.0,120.0,145.0,130.0,152.0,144.0,175.0,180.0,135.0,140.0,178.0,191.0,137.0,189.0,55.0,70.0,75.0,65.0,74.0,80.0,84.0,79.0,90.0,98.0,95.0,108.0,113.0,110.0,125.0,115.0,130.0,135.0,120.0,140.0,140.0,152.0,140.0,137.0,145.0,175.0,189.0,180.0,178.0,191.0);
x:=array((80.0),(100.0),(85.0),(110.0),(120.0),(115.0),(130.0),(140.0),(125.0),
(90.0),(105.0),(160.0),(150.0),(165.0),(145.0),(180.0),(225.0),(200.0),(240.0),
(185.0),(220.0),(210.0),(245.0),(260.0),(190.0),(205.0),(265.0),(270.0),(230.0),
(250.0),(80.0),(85.0),(90.0),(100.0),(105.0),(110.0),(115.0),(120.0),(125.0),
(130.0),(140.0),(145.0),(150.0),(160.0),(165.0),(180.0),(185.0),(190.0),(200.0),
(205.0),(210.0),(220.0),(225.0),(230.0),(240.0),(245.0),(250.0),(260.0),(265.0),
(270.0));
wweight:=1/(x[:,0]^1.5);
Return Regression_WLS(Y,X,0.05,1,1,nil,nil,nil,wweight);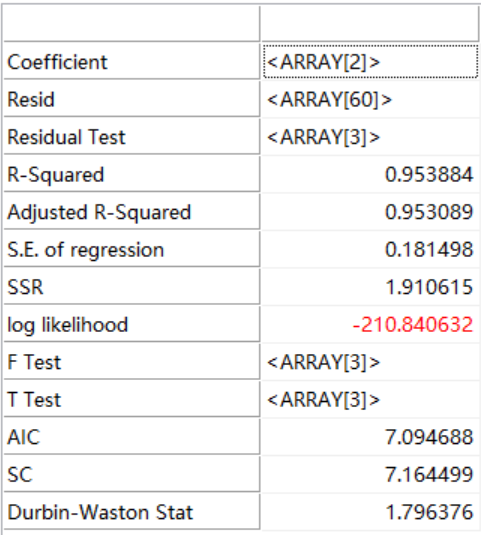
相关