天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验
Regress_pri
简述
主成分回归,利用解释变量(Z 分数标准化)进行主成分分析降维得到的主成分,来对被解释变量(Z分数标准化)进行回归,进而消除多重共线性定义
Regress_pri(Y:Array of Real;X:Array of Real;Exps:Real;Alpha:Real):Array
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| Y | Array of Real | 被解释变量序列,为一维数组类型 |
| X | Array of Real | 解释变量矩阵,为二维数组类型,每一列为一个解释变量 |
| Exps | Real | 主成分累计贡献率,作为选取主成分数目的依据,当为小数时,代表累计贡献率的阀值,比如0.85,当为整数时,代表取的主成分的个数,比如2表示取前2个主成分。 |
| Alpha | Real | 显著性水平,实数或整数,在01之间 |
- 范例
解释变量1 解释变量2 解释变量3 解释变量4 解释变量5 解释变量6 1.431 0.424 28.439 182.3 110.831 -293.756 1.651 0.318 33.287 250.835 152.497 -162.076 1.027 0.003 22.314 209.87 127.592 -153.508 1.081 0.001 24.029 176.446 107.272 -142.257 1.117 0.164 25.75 145.37 88.379 -294.591 1.484 0.188 32.626 166.437 101.187 -360.097 1.325 0.442 25.108 173.032 105.196 -327.462 1.519 0.804 27.114 183.501 111.561 -289.782 1.329 0.621 20.759 113.244 68.848 -658.805 1.02 0.549 16.086 114.542 69.637 -619.165 1.209 0.633 19.215 150.918 91.752 -194.209 1.573 0.741 24.169 210.993 128.275 -133.067 0.943 0.6 14.548 204.009 124.029 -155.778 0.829 0.667 12.946 204.971 124.614 -134.152 0.927 0.812 14.594 398.204 242.091 -122.255 0.167 0.61 2.422 286.634 174.261 -133.654 -0.293 0.49 -4.122 89.503 54.414 -236.781 -0.446 0.576 -6.198 -66.142 -40.212 -56.116 -0.053 0.571 -0.716 44.514 27.063 611.885 -0.133 0.213 -1.783 -51.718 -31.442 -41.645 -0.039 0.367 -0.536 -102.793 -62.494 -58.664 0.181 0.409 2.751 -16.555 -10.065 -18.585 0.025 0.16 0.442 -66.158 -40.221 -47.71 -0.134 0.22 -1.817 -159.184 -96.777 -68.74 0.045 0.155 0.85 -20.311 -12.348 -21.893 0.059 0.076 1.038 -52.438 -31.88 -41.981 -0.188 0.006 -2.626 -50.366 -30.62 -34.58 0.354 0.114 5.15 140.769 85.582 -206.032 0.324 -0.242 6.233 291.18 177.026 -148.341 解释变量7 解释变量8 解释变量9 解释变量10 解释变量11 被解释变量 -576.35 3038.437 1847.244 -8949.161 -17558.29 0.6 -282.297 3992.413 2427.222 -6484.493 -11294.439 0.667 -418.446 2704.007 1643.925 -4163.383 -11348.898 0.812 -1260.496 2281.625 1387.134 -3257.498 -28863.787 0.61 605.611 2095.182 1273.784 -6196.863 12739.329 0.49 1117.915 2610.283 1586.944 -9428.13 29269.472 0.576 2568.14 2626.929 1597.064 -8628.615 67670.492 0.571 -11379.056 2724.996 1656.685 -7920.047 -311001.92 0.213 185.692 1834.922 1115.557 -12147.208 3423.841 0.367 233.605 1857.328 1129.179 -11556.339 4360.099 0.409 9312.993 2205.132 1340.629 -4298.943 206149.543 0.16 -338.246 2781.867 1691.26 -3712.606 -9437.154 0.22 -298.984 2363.908 1437.159 -3695.792 -7093.291 0.155 -224.157 2133.811 1297.269 -2874.695 -4803.394 0.076 -144.225 2633.445 1601.026 -3230.017 -3810.463 0.006 -202.274 1925.562 1170.662 -2588.069 -3916.818 0.114 228.624 1661.155 1009.914 -3992.523 3854.983 -0.242 -31.182 612.07 372.113 -336.585 -187.029 -0.255 42.943 1629.952 990.943 10256.156 719.794 -0.248 -25.383 919.83 559.218 -373.312 -227.538 -0.042 -40.435 903.872 549.517 -523.253 -360.658 -0.181 -9.953 991.052 602.519 -170.109 -91.103 -0.274 -30.643 1038.49 631.359 -485.897 -312.083 -0.169 -52.728 856.257 520.569 -583.427 -447.526 -0.11 -12.573 1144.935 696.073 -234.303 -134.559 -0.079 -27.054 1138.099 691.917 -465.796 -300.176 -0.025 -25.356 1008.787 613.301 -339.702 -249.089 0.095 -2097.228 1472.114 894.984 -3061.924 -31167.74 0.185 -197.858 1757.787 1068.662 -2622.88 -3498.408 0.358
return s:= regression(y,x,0.05,1);
tr:=s["Coefficient"];
return x:*(`(tr[1:length(tr)-1]))+tr[0] | y;
//预测效果图: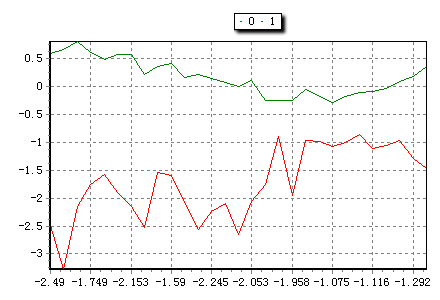
R:=corr(x,1);//检验多重共线性
return regress_vif(X);
//array("VIF":(0.508,0.452,0.166,0.00,0.00,0.324,2.405,
//2.428,0.401,0.292,7.472),"Cond":INF)
s:=regress_pri(y,x,0.85,0.05);//主成分回归
//return s;
tr:= s["Coefficient"];
return x:*(`(tr[1:length(tr)-1]))+tr[0] | y; //主成分回归预测值与实际值的比较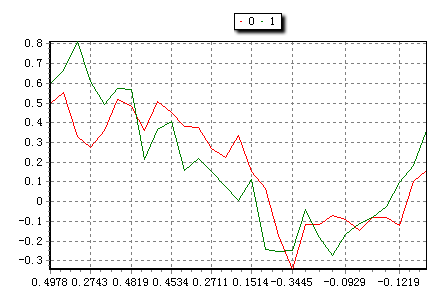
主成分回归结果: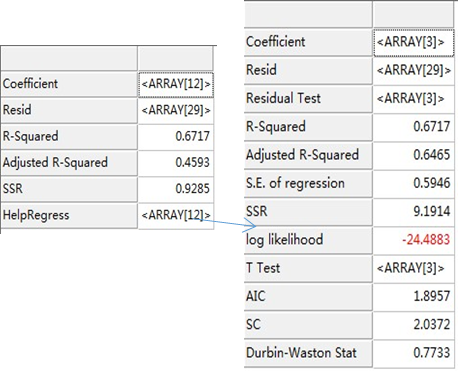 Regression Regress_Ridge Regress_Stepwise Regress_VIF boxcox参考
Regression Regress_Ridge Regress_Stepwise Regress_VIF boxcox参考
相关