天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验
在单因子有效性的检验中,进行检验的往往是组合收益率序列或者因子收益率序列在
时序上是否显著异于零,这一过程本身并不涉及回归过程,因此无法直接使用上一节中介绍的调整方法。然而,我们知道组合收益或者因子收益在时序上极有可能存在异方差和自相关特性,因此在计算序列标准误时,必须对其进行 Newey-West 调整,从而得到其标准差的一致性估计,进而得到更稳健的 t 值。
关于这个问题Bali et al(2016)指出对于单个因子收益率序列的显著性检验,我们可以将其转换为一个简单的线性回归模型:将 1 作为自变量,将因子收益率作为因变量,进行回归得到残差变量。此时残差项即为因子收益率减去它在时间序列上的均值。把残差项和X=1代入即可得到简化的结果,对Q的估计形式如下:QNW-Simple=1Tt=1Tet2+l=1Lt=l+1Twletet-l
其中,wl=1-l1+L
这里的Q实际上不是矩阵,只是一个数。
将Q代入Cov[β*]中就可以求出收益率方差的估计,之后就可以进行T检验了。σ2=QNW-Simple/T
NW_Adjustment_Simplification
简述
在单因子有效性的检验中,进行检验的往往是组合收益率序列或者因子收益率序列在
时序上是否显著异于零,这一过程本身并不涉及回归过程,因此无法直接使用上一节中介绍的调整方法。然而,我们知道组合收益或者因子收益在时序上极有可能存在异方差和自相关特性,因此在计算序列标准误时,必须对其进行 Newey-West 调整,从而得到其标准差的一致性估计,进而得到更稳健的 t 值。
关于这个问题Bali et al(2016)指出对于单个因子收益率序列的显著性检验,我们可以将其转换为一个简单的线性回归模型:将 1 作为自变量,将因子收益率作为因变量,进行回归得到残差变量。此时残差项即为因子收益率减去它在时间序列上的均值。把残差项和X=1代入即可得到简化的结果,对Q的估计形式如下:QNW-Simple=1Tt=1Tet2+l=1Lt=l+1Twletet-l
其中,wl=1-l1+L
这里的Q实际上不是矩阵,只是一个数。
将Q代入Cov[β*]中就可以求出收益率方差的估计,之后就可以进行T检验了。σ2=QNW-Simple/T
定义
NW_Adjustment_Simplification(y:Array;alpha:Real;AL:Integer):Array
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| y | Array | 一维数字数组, 因变量 |
| alpha | Real | 实数,显著性水平,应为0到1之间的值,默认0.05 |
| AL | Integer | 整数,自相关最大滞后阶数,可缺省,默认用Newey and West (1994)?提出的方法计算,至少为1 |
| 返回 | Array | 数据表, 检验结果 |
- 范例y:=array(0.001,0.56,0.193,0.80,0.58,0.48,0.35,0.89,0.82,0.74);
return NW_Adjustment_Simplification(y);
//返回: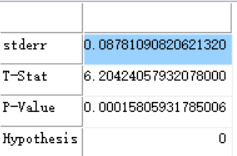
相关