天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验
Regress_NLM
简述
多元非线性回归,采用Marquardt方法求多元非线性方程的最小二乘回归系数。定义
Regress_NLM (Func:string; x:Array of Real;y:Array of Real;Initial:array) :array
参数
| 名称 | 类型 | 说明 |
|---|---|---|
| Func | string | 回归方程函数名,为字符串类型 |
| X | Array of Real | 解释变量矩阵,为二维数组类型,每一列为一个解释变量 |
| Y | Array of Real | 被解释变量序列,为一维数组类型 |
| Initial | array | 估计参数初始值,一维数字数组 |
| 返回 | array | 数组
各字段解释:[Coefficient]:估计参数 [residuals]:残差序列 [Jacobian]:雅可比矩阵 [sse]:残差平方和 [Fitted]:拟合值 [contrast]:Y和拟合值对比 |
- 范例
年份 消费价格指数CPI X1(以1978年为100) 人均可支配收入 X2(元) 上年人均消费支出 X3(元) 人均消费支出 Y(元) 1993 273.100 2577.400 1671.730 2110.810 1994 339.000 3496.200 2110.810 2851.340 1995 396.900 4283.000 2851.340 3537.570 1996 429.900 4838.900 3537.570 3919.470 1997 441.900 5160.300 3919.470 4185.640 1998 438.400 5425.100 4185.640 4331.600 1999 432.200 5854.020 4331.600 4615.900 2000 434.000 6280.000 4615.900 4998.000 2001 437.000 6859.600 4998.000 5309.000 2002 433.500 7702.800 5309.000 6029.880 2003 438.700 8472.200 6029.880 6510.940 2004 455.800 9421.600 6510.940 7182.100 2005 464.000 10493.000 7182.100 7942.880 2006 471.000 11759.500 7942.880 8696.550 2007 493.600 13785.800 8696.550 9997.470
回归方程: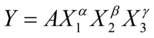
Y1:=log(Y);
X1:=log(X);
return Regression(Y1,X1);
注:根据Hypothesis,0表示显著,1表示不显著,则T检验最后一个变量通不过!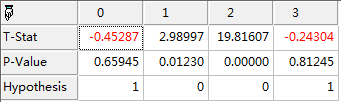
return Regress_VIF(x1); // array("VIF":(7.83,66.409,95.241),"Cond":269.959)
注:当VIF>10或Cond>30时,认为存在严重的多重共线性,第1,2个变量存在严重多重共线性,?第1,2个变量影响是相似的,则可以降维减少特征数量。
return Regress_Stepwise(Y1,X1,0.05,0.1)//逐步回归选取第0,1个解释变量
逐步回归结果: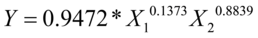
x:=x[:,0:1];
return Regress_NLM('Demo_Regress_NLM_CallBack',x,y,array(-0.2,0.2,0.8));或
return Regress_NLM('Demo_Regress_NLM_CallBack',x,y, array(-0.1,0.2,0.9));
其中Demo_Regress_NLM_CallBack函数
Function Demo_Regress_NLM_CallBack(beta,x);
Begin
return beta[0]*(x[0]^beta[1])*(x[1]^beta[2]);
End;
结果都是: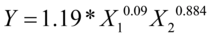

估计参数残差序列雅克比矩阵(解释变量)可决系数拟合值拟合值和实际值的比较Regress_CMLS Regression Regress_Binary参考
相关