天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验

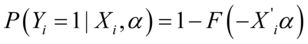
Regress_Binary    

简述
二元离散选择模型。返回结果有方程的系数、负2倍对数似然值和Wald检验（原假设为解释变量对被解释变量影响不显著，检验包含统计量、P值和原假设的值1表示接受原假设，0表示拒绝原假设）
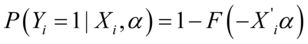
定义
Regress_Binary (Y:Array of Real;X:Array of Real;Extimation:String;Methods:int;Constant:Boolean;Alpha:Real):Array
参数
名称类型说明
YArray of Real二元离散被解释变量序列，为一维数组类型
XArray of Real解释变量矩阵，每一列为一个解释变量，为二维数组类型
ExtimationString 模型选择，字符串类型，"logit"或"probi"
Methodsint0:单纯形法，1:转轴法,2:模式搜索法, 3:拟牛顿下山法,一般使用3方法
ConstantBoolean是否包含常数项，为布尔类型，缺省为true
AlphaReal显著性水平，实数类型，取值在0-1之间，缺省时只输出模型的估计
  • 范例

    在一次关于某城镇居民上下班使用交通工具的社会调查中，因变量y =1表示居民主要乘坐公共汽车上下班；y=0表示主要骑自行车上下班；自变量x1表示被调查者的年龄；x2表示被调查者的月收入；x3表示被调查者的性别（x3=1为男性，x3=0为女性）
    交通工具 年龄 月收入 性别 交通工具 年龄 月收入 性别
    0 18 850 0 0 20 1000 1
    0 21 1200 0 0 25 1200 1
    1 23 850 0 0 27 1300 1
    1 23 950 0 0 28 1500 1
    1 28 1200 0 1 30 950 1
    0 31 850 0 0 32 1000 1
    1 36 1500 0 0 33 1800 1
    1 42 1000 0 0 33 1000 1
    1 46 950 0 0 38 1200 1
    0 48 1200 0 0 41 1500 1
    1 55 1800 0 1 45 1800 1
    1 56 2100 0 0 48 1000 1
    1 58 1800 0 1 52 1500 1
    0 18 850 1 1 56 1800 1

    使用极大似然法估计模型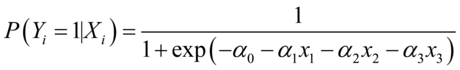中的各个参数：
    y:=array(0.00,0.00,1.00,1.00,1.00,0.00,1.00,1.00,1.00,0.00,1.00,1.00,1.00,0.00,0.00,0.00,0.00,0.00,1.00,0.00,0.00,0.00,0.00,0.00,1.00,0.00,1.00,1.00);
    x:=`array((18,21,23,23,28,31,36,42,46,48,55,56,58,18,20,25,27,28,30,32,33,33,38,41,45,48,52,56),(850,1200,850,950,1200,850,1500,1000,950,1200,1800,2100,1800,850,1000,1200,1300,1500,950,1000,1800,1000,1200,1500,1800,1000,1500,1800),(0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1));
    constant:=true;
    alpha:=0.05;
    ret:=Regress_Binary(y,x,"logit",3,constant,alpha);

    结果：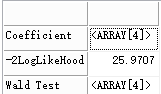

    下面我们继续看看样本内的误判率：
    a:=(ones(length(x))|x):*`ret["Coefficient"];
    a::=1/(1+exp(-mcell));
    a:=a[:,0];
    a::=mcell>=0.5;
    //预测值
    //return y|a;
    b:=y-a;

    //误判的为0或1
    b::=abs(mcell);
    return sum(b)/length(b);

    得到的结果：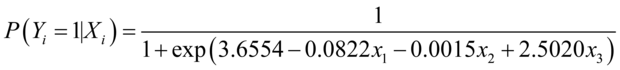
    阈值设为0.5，误判率是0.17857
    参考
    Regress_CMLS Regression Regress_NLM 
相关