天软金融分析.NET函数大全 > TSL函数 > 数学函数 > 回归 > 回归检验

Regress_Constraint    

简述
线性约束最小二乘回归
定义
Regress_Constraint(Y;X:Array of Real;Constant: Boolean;A;B;Aeq; Beq: Array of Real;Alpha: Real;Options:Integer;Lb: Array of Real;ub: Array of Real);
参数
名称类型说明
YArray of Real 被解释变量序列，为一维数组类型，不可缺省
XArray of Real 解释变量矩阵，为二维数组类型，每一列为一个自变量，不可缺省
Constant Boolean是否包含常数项，为布尔类型
A Array of Real 不等式约束二维数字数组，不可缺省
B Array of Real 不等式约束一维数字数组，不可缺省
Aeq Array of Real 等式约束二维数字数组
beq Array of Real 等式约束一维数字数组
Alpha Real显著性水平，实数或整数，在0与1之间，缺省时只做参数的估计
OptionsInteger 方法选择: 0 残差平方和最小；1 方差最小
Lb Array of Real下界约束一维数组
Ub Array of Real上界约束一维数组
返回数组，具体下标对应的值如下：
Coefficient:回归方程系数，若Constant为1，第0行为常数项。
Fval:目标值，Constant :0为残差平方和，1为方差
R-Squared:R方
Adjusted R-Squared:调整的R方
Residual Series:残差序列
Residual Test: 残差的正态检验
      JB-Stat: Jarque-Bera统计值

P-Value: p值

Hypothesis: 原假设的值
F TEST: 方程的F检验, Constant为1才进行此检验。
    F-Stat: F统计值

P-Value: p值

Hypothesis: 原假设的值
T TEST: 回归系数的T检验。
    T-Stat: T统计值

P-Value: p值

Hypothesis: 原假设的值
Durbin-Waston Stat: DW统计量
Info Criterion: 信息准则函数Aic和Sbic
  • 范例

    y := array(0.425306623295765,1.36119535984939,0.330434097687351,0.693363166256445, 1.12135794381143,0.992864415538359,0.599585222220468,1.03157839185033,0.817720425216125,0.613581071515125);
    x := array( (0.0437987553887069,0.865901106735691,0.637902588583529),
    (0.991149639012292,0.402538175228983,0.830022667301819), (0.794031135737896,0.866388283902779,0.336671882774681),
    (0.715198307996616,0.416468291543424,0.581486012088135),
    (0.0273062069900334,0.24702803301625,0.983555873855948),
    (0.529860897222534,0.200076438020915,0.59641290246509),
    (0.813422230072319,0.370269910665229,0.23934360453859),
    (0.888038919074461,0.293901670724154,0.613906089449301),
    (0.311180313583463,0.752806227421388,0.332180465571582),
    (0.31012851675041,0.979520652908832,0.346078625647351)) ;
    constant := 1;// 包含常数项
    a := array();
    b := array();
    aeq := array((1,1,1)); //加入等式约束，之和为 1.2
    beq := array(1.2);
    alpha := 0.05; 
    option:=0;// 残差平方和最小
    lb:=array();
    ub:=array();
    return Regress_Constraint(y,x,constant,A,b,aeq,beq,alpha,option,lb,ub);

    返回结果：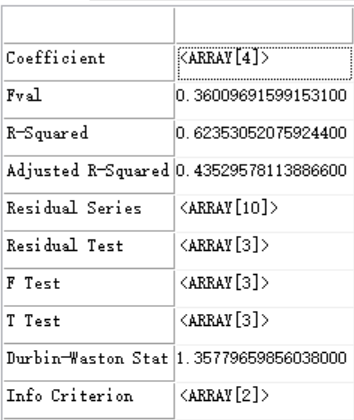
    参考
    Regress_CMLS Regression Regress_NLM Regress_Binary 
相关